Pierre CRESPIN
Etude sur le quinzième pavage pentagonal du plan
EnAttente
Quelques autres nouvelles figures en attente.
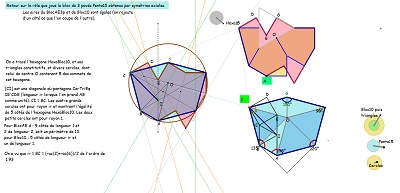
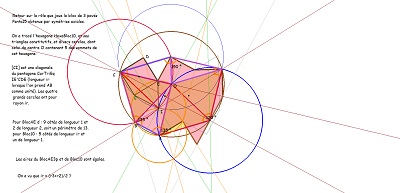
Retours sur le lien entre Bloc 3p et Bloc10 (Hexa10 par la suite)!
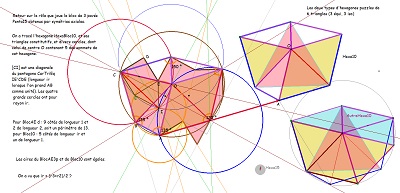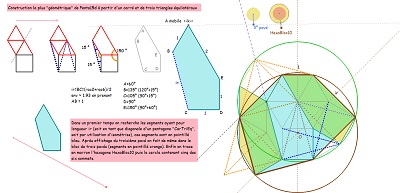
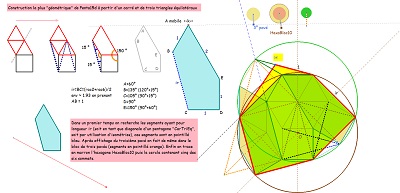
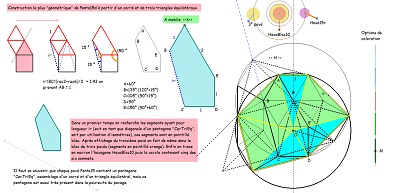
Un nouveau retour sur la création de Penta15, puis sur celle de Hexa10 et une tentative pour évaluer la cohérence de tout cela
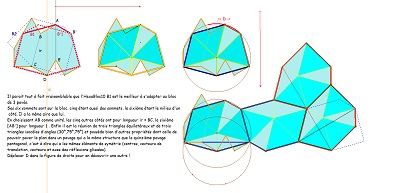pavage de rosaces de Diane, essai de coloration
En prolongement de figures très intéressantes du site de Mr DEBART (Descartes et les Mathématiques) à propos de carrés et triangles équilatéraux (deux "CarTriEq", nom barbare que j'ai donné à cette paire). je pense cette fois que les liens entre Penta15 et d'autres figures est bien établi.
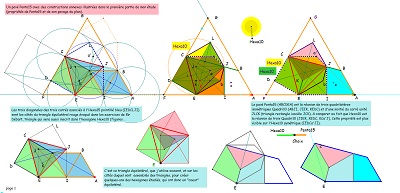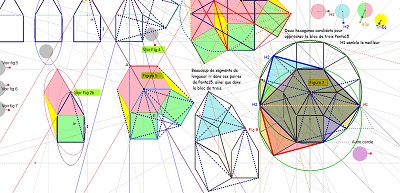
Dans le même ordre d'idée : une autre approche de Penta15 comme hexagone particulier ayant 5 côtés sur 6 isométriques, et avec utilisation de paires "carré-triangle équilatéral"
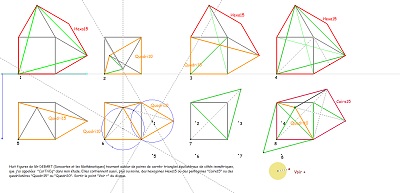
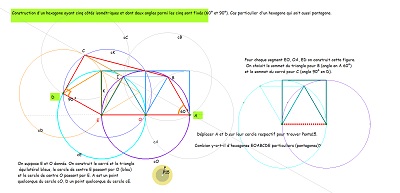toujours sur le thème carrés-triangles équilatéraux
avec un Penta15 qui serait l'enveloppe convexe d'un assemblage de CarTriEq

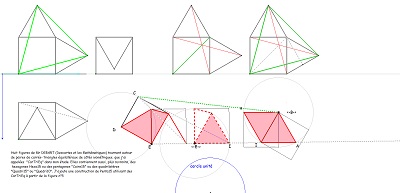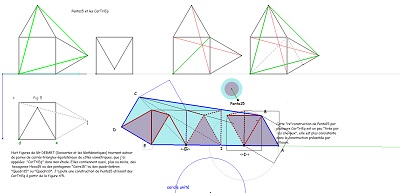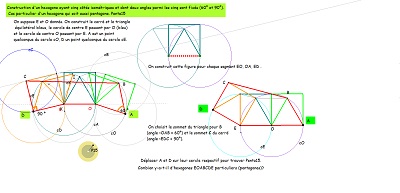
Rosaces, Hexa10 ou HexaBloc10 et pavages

en complément de cette première figure déjà présentée ----------->

Voir aussi en complément PavageRosaces10

 


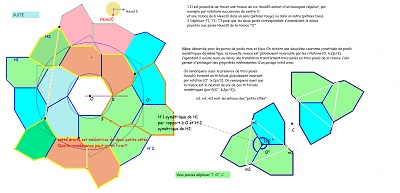à compléter éventuellement par

2021 NewBloc10Hexa15bis.html

2021 NewBloc10Hexa15autrebis.html

2021 NewBloc10Hexa15AutrePlus.html

pour voir les pavages sur une large partie
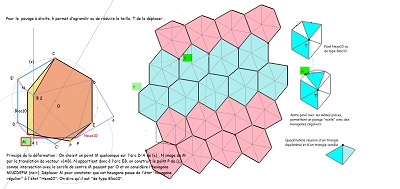
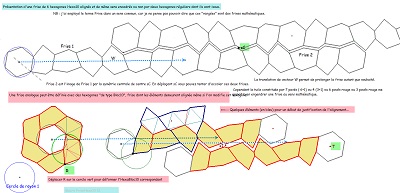
Hexa10 et HexaBloc10 permettent de construire des rosaces autour d'un hexagone régulier (comme ci-dessus) et aussi des "frises" rectilignes (comme ci-contre). Voir le lien entre ces images.
De nouveaux projets de découpe pour puzzles ...
en cours... Puzzles15.html
  
   
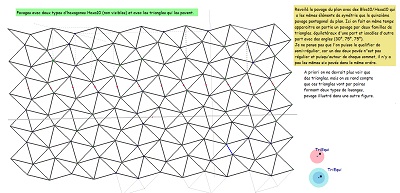
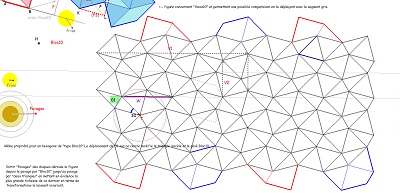
Parmi les pavages avec des hexagones de type Bloc10, celui par Hexa10 est bien le seul ayant les mêmes éléments de symétrie que le quinzième pavage pentagonal du plan. Constatation avec la comparaison des normes des deux vecteurs de base. Vérification pour les symétries glissées sur le pavage "2 triangles".
Retour sur les choix possibles dans la formation du pavage par Hexa10
Et une bonne raison à partir des pavages par des triangles équilatéraux et triangles isocèles
en constatant qu'un espoir de plus de périodicité est incité par un changement de sens
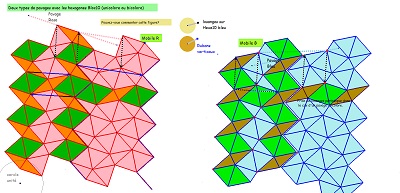
Rubans de losanges dans les pavages unicolores
et dans le pavage bicolore ci-dessous ! ( mieux )
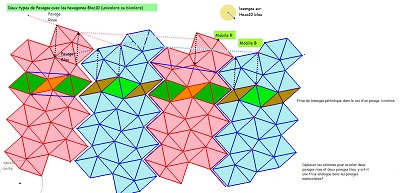
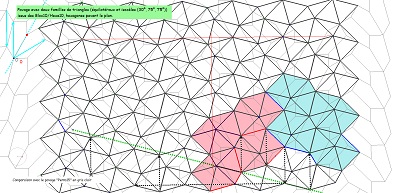
Illustration de l'existence d'une translation qui laisse des frises invariantes dans le pavage "deux triangles" issu du pavage par Hexa10/Bloc10 ayant mêmes éléments de symétrie que le pavage Penta15 (pavage bicolore par les Hexa10). Comparaison pavage "deux triangles", pavage "Penta15".
   
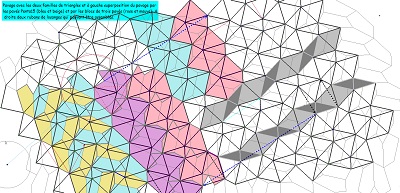
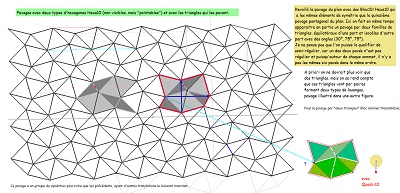
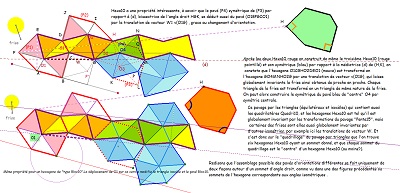
Ces dernières figures explicitent plus nettement le pourquoi des diverses impressions émises à propos d'un multiple pavage par les pavés Hexa10 ou de "type Bloc10". Si l'on "efface" les hexagones Hexa10 ou Bloc10 qui ont conduit au pavage par les "deux triangles", il est possible, sur le "quadrillage-maillage triangulaire", de trouver plusieurs hexagones Hexa10 (Bloc10) ayant un centre donné, et plusieurs (six) hexagones Hexa10 (Bloc10) ayant un sommet donné. Rappelons aussi que chaque noeud du maillage est l'extrémité de six segments dont cinq sont isométriques, ce point est donc le centre d'un cercle contenant cinq sommets.
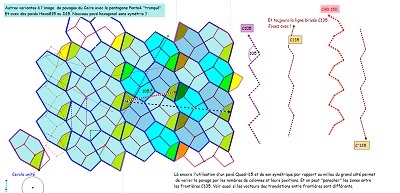
Autre pavage, cette fois en tronquant un quadruplet de pavés du Caire "version Caire15", ce qui crée une liaison possible par quadrilatère "Quadri15"; même démarche pour les pavages par les Bloc3p.
le pavé du Caire "tronqué" est un hexagone qui pave le plan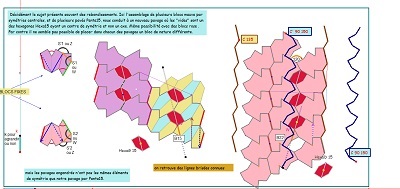
l'existence de la frontière ZigZag d'angles droits et les divers pavages que l'on peut construire avec les Hexa10 avec insertion ou non de colonnes de carrés.


Références :
J'avais affirmé au début de mon étude n'avoir pu consulter beaucoup de documents sur le sujet en dehors de ceux que je citais. Je n'étais pas encore bien rompu à ces recherches. Après quelques mois (années?) passés, il me semble avoir pu consulter de nombreux documents intéressants en liaison avec les pavages, dont les pavages pentagonaux ou/et hexagonaux. Cette liste est présentée ici : bibliographie .
J'ai pu constater que deux ou trois des éléments auxquels je me suis intéressé figurent dans les travaux consultés et sont antérieurs à mon étude, mais j'y étais parvenu indépendamment. Et cela me confirme dans mon analyse que le sujet est riche. Les emprunts ou prolongements sont à priori indiqués. Merci de me contacter en cas de problème.

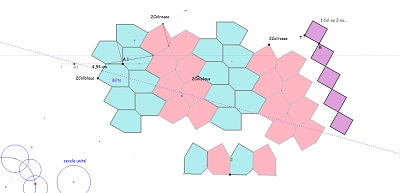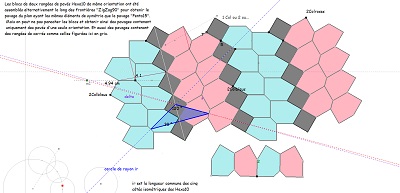Quelques idées pour la suite ???, activités possibles :
- approfondir l'étude des pavés "presque équilatéraux" (ils sont déjà assez nombreux dans cette étude, est-ce par hasard ?)
- retrouver les caractéristiques de pavés pentagones à partir d'images de pavages trouvées sur Internet.
- approfondir l'étude des pavages de Marjorie Rice, avec une construction vue pour les pavés équilatéraux,
- revoir certaines propriétés de ces pavages, en distinguant les orientations des pavés comme fait pour le pavage "Penta15".
- La rencontre avec le pavage de la rosace de Diane semble aussi à approfondir. (page en cours provisoire RosaceDiane.html )
 
suite et presque fin (TousLesPavages)
Sommaire Partie II ou Sommaire 2020 Penta15 ou sommaire Penta15
Conclusion Partie2
mais aussi ...
Rapide présentation de l'étude sur "Orange"
Résumé en 10-15 figures
Résumé en 45-50 figures
sommaire Penta15 (étude complète)
en cours de mise au point
? diaporamas (chez Google ou avec Powerpoint)