Puzzles15

Ces images montrent que trois et même quatre hexagones parmi d'autres, sont fabriqués à partir d'un triangle équilatéral en lui adjoignant des triangles sur les trois côtés. C'est évident pour l'hexagone régulier bien sûr, bien que l'on pense à priori plutôt à l'égalité des angles et des côtés pour le définir. Dans la figure suivante on voit que c'est aussi le cas pour Hexa15, qui apparait ici comme ayant une propriété partagée avec l'hexagone régulier, et les deux Hexa10 en ajoutant deux triangles rectangles isocèles sur deux côtés et un autre triangle parmi les trois possibles figurant dans le triangle central.
Raison de plus pour poursuivre autour de cette idée d'adjonction de trois triangles sur un triangle "intérieur" ( équilatéral ou autre). ...

Pierre CRESPIN	page provisoire en cours de reprise		Puzzles15.html
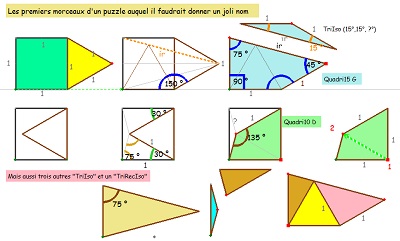
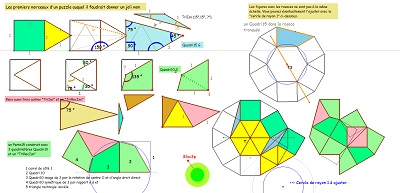
Un certain nombre de polygones ou de figures étudiés sont assemblages de quelques pièces de base . On essaie de faire une synthèse de ces situations.

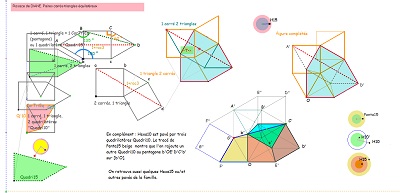
La première figure est la réunion d'un carré et d'un triangle équilatéral de côtés isométriques, figure que j'ai appelée "CarTriEq" qui donne naissance à un pentagone (qui pave le plan), à un quadrilatère "Quadri15" et un triangle isocèle d'angles (15°,15°,150°). Une autre paire CarTriEq donne naissance à un quadrilatère "Quadri10", qui est l'assemblage d'un triangle isocèle et un triangle rectangle isocèle. On peut déterminer les divers éléments (longueurs, mesures d'angle). Quadri10 est l'assemblage d'un triangle équilatéral et d'un triangle isocèle (30°,75°,75°), et le quadrilatère Quadri15 est aussi l'assemblage donc d'un Quadri10 et d'un triangle rectangle isocèle (moitié du carré).
Montrons rapidement le lien avec le pentagone "Penta15" ainsi qu'avec la rosace de Diane et les blocs de trois pavés Penta15 en complétant la figure. Vous constatez que Penta15 est déjà obtenu de trois manières comme puzzle utilisant des pièces parmi les précédentes.
D'autres figures dont les hexagones Hexa15 à partir de deux quadrilatères Quadri15 dont il est l'assemblage par réflexion, les deux autres hexagones étant eux obtenus par symétries centrales. par rapport au milieu du grand côté. Ces trois hexagones sont équilatéraux.
on retrouve certains d'entre eux dans les rosaces de Diane qui devient une bonne source de création
l'hexagone Hexa10 est issu de l'hexagone Hexa15 ou d'un bloc de trois pavés Penta15 , il a la même aire que celui-ci; et il est aussi pavé par trois quadrilatères Quadri10 et donc par trois triangles équilatéraux et trois triangles isocèles (30°,75°,75°)
En attendant quelques autres modifications je laisse les figures suivantes (à reprendre) qui montrent certaines propriétés du même ordre.

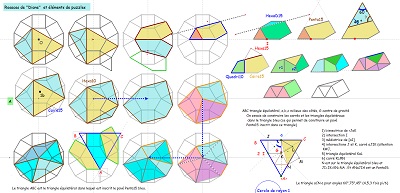
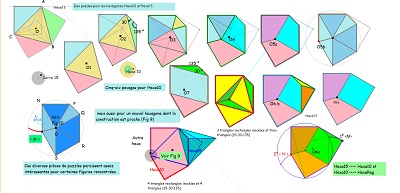
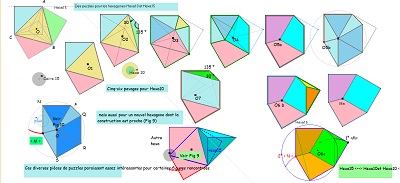
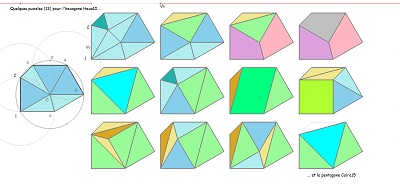
d'autres éléments pour Hexa15 et un autre hexagone à partir d'une figure vue sur internet
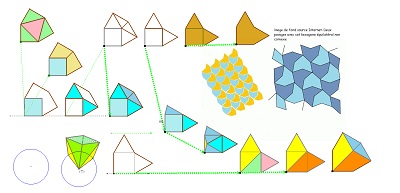
Un document très intéressant dans le Petit Vert de l'APMEP de Lorraine et mes propres digressions sur le sujet.
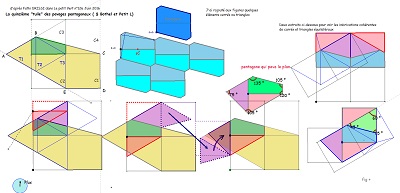
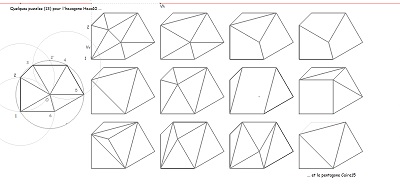
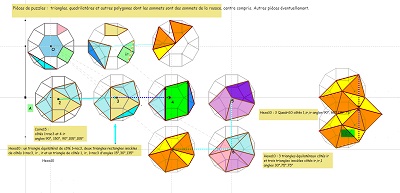
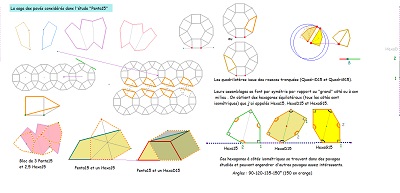
Liste des éléments de la famille Penta15, Hexa15, Caire15, Hexa10 ou HexaBloc10 que l'on retrouve dans les puzzles de ces figures On rappelle que, à priori, on choisit pour unité de longueur le côté du triangle équilatéral et du carré de base aussi bien dans la rosace de Diane que dans le pavé Penta15. On rappelle aussi qu'alors les diagonales de la paire "CarTriEq" ont pour mesure le nombre que j'ai appelé "ir", égal à (rac2+rac6)/2 ou encore 2 cos(pi/12) ~ 1,93. Parmi les figures de la saga15 à partir du pavé Penta15, quinzième pentagone pavant le plan, il y a tout d'abord bien sûr les carrés, triangles équilatéraux de côté 1, puis les quadrilatères Quadri15 G ou D de côtés (1,1,1,ir), l'hexagone régulier de côté 1 ainsi que sa moitié, les triangles isocèles (15°,15°,150°) de côtés (1,1,ir) ou (75°,75°,30°) et de côtés ( , , ) , hexagones Hexa15 de côtés 1 , de côtés ir, hexagones Hexa10 de côtés (1,ir,ir,ir,ir,ir),quadrilatères Quadri10 G ou D de côtés 1,ir,ir,ir, qui sont assemblages de deux triangles, un équilatéral de côtés ir , l'autre isocèle de côtés ir,ir,1. Un Hexa10 est l'assemblage de trois Quadri10, deux de même orientation et le troisième de sens différent. Un Hexa10 est donc l'assemblage de trois triangles équilatéraux de côtés ir,ir,ir et de trois triangles isocèles (de côtés ir,ir,1 et d'angles 30°,75°,75°). Il faut aussi évoquer l'assemblage, autour d'un parallélogramme, avec deux triangles , l'un rectangle isocèle ( côtés ir,ir,ir.rac2), l'autre d'angles 15°,30°,135° et de côtés (1,ir,ir.rac2) Des figures semblables peuvent aussi être rencontrées ; on précisera éventuellement l'échelle en cas d'ambiguïté. Les longueurs et distances sont alors proportionnelles.
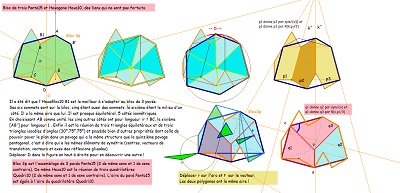
Le pavé Penta15 est inscrit dans un triangle équilatéral, le triangle d'angles (45°,60°,75°) est un élément qui pave un hexagone Hexa15 par réflexions successives -->
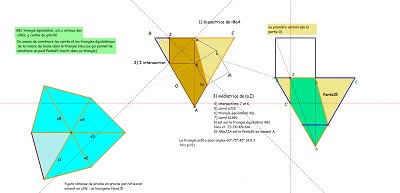
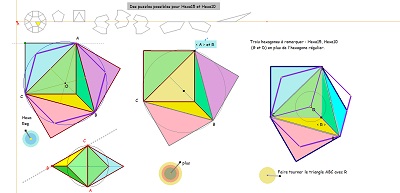
Penta15 et Hexa15
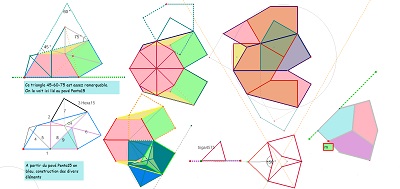
Des puzzles pour Hexa10, Caire15 et Hexa15, Hexa10 et ... Penta15 avec des pièces communes.

à venir ... des puzzles avec un ensemble de pièces, dont ces divers éléments ... Hexagones autour d'un triangle équilatéral
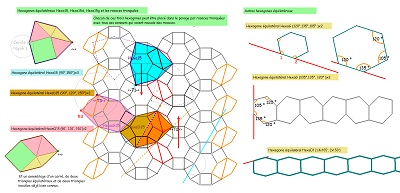
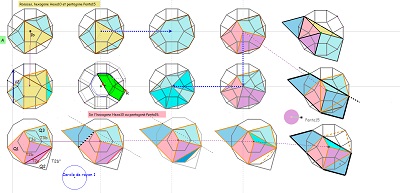
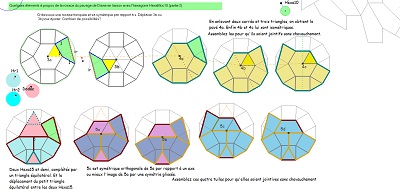
Ces images montrent que trois et même quatre hexagones parmi d'autres, sont fabriqués à partir d'un triangle équilatéral en lui adjoignant des triangles sur les trois côtés. C'est évident pour l'hexagone régulier bien sûr, bien que l'on pense à priori plutôt à l'égalité des angles et des côtés pour le définir. Dans la figure suivante on voit que c'est aussi le cas pour Hexa15, qui apparait ici comme ayant une propriété partagée avec l'hexagone régulier, et les deux Hexa10 en ajoutant deux triangles rectangles isocèles sur deux côtés et un autre triangle parmi les trois possibles figurant dans le triangle central. Raison de plus pour poursuivre autour de cette idée d'adjonction de trois triangles sur un triangle "intérieur" ( équilatéral ou autre). ...
PLUS : Compléments éventuels non indispensables
Retour Compléments en attente		Retour rosaceDiane.html	suite HexagonesRencontres.html
		sommaire Penta15 ou Sommaire 2020 Penta15	Conclusion Partie2