rosaceDiane

Penta15 et rosace de Diane

la considération d'une paire de pavés Penta15 nous conduit à l'introduction d'une rosace de Diane ...

... ou plutôt de l'une ou l'autre de deux rosaces.

on reconnait aussi l'hexagone Hexa10 ... et son pavage par des triangles vus par ailleurs

toujours en travaux et à reprendre

Première fois où apparait un pavé Penta15 (grand) dans une rosace de Diane dont une couronne est obtenue par symétries successives de blocs de trois pavés Penta15. ^^

Cette rosace de Diane est bien la figure par laquelle il aurait fallu commencer ! Le bloc de trois pavés Penta15 s'adapte assez bien à elle et l'hexagone Hexa10 a tous ses sommets qui en sont aussi sommets, il en est donc un sous-ensemble. Une paire de pavés Penta15, visibles si l'on trace deux segments "diagonaux", "de travers",! et même un trio de pavés ... ainsi que des pavés divers rencontrés dans cette étude se trouvent bien présents (voir aussi les figures ci-dessous).

Découverte de nombreux éléments d'une assez grande diversité (ou peut-on parler de richesse ?) en cours de modification

^^ Rosaces et pentagones Penta15

Assemblages possibles de rosaces de Diane ou de rosaces issues de rosaces de Diane dont des rosaces "tronquées"

On a été amené souvent à choisir un mode d'assemblage pour des blocs ou pour les rosaces étudiées. On essaie de faire le point sur les divers cas rencontrés pour les rosaces de Diane, mais aussi pour d'autres tuiles comme les rosaces tronquées, dont la présence a été assez naturelle dans certains cas (ou pour des parties de ces rosaces).

Pour tester la meilleure position relative d'un des deux blocs de 3 Penta15, de l'Hexa10 et de la rosace support ---- >> à revoir quel intérêt ici ??

Dispositions relatives de rosaces et de blocs de trois pavés avec assemblage de deux blocs symétriques orthogonaux. Blocs déjà évoqués, comparés à la rosace la plus adaptée

pavage rosaces de Diane v

pavage avec les deux pour comparaison

pavage rosaces de Diane tronquées v

suite (PavageRosaces10.html)

PLUS (Compléments en réserve, page qui peut être négligée)

En prolongement de figures très intéressantes du site de Patrice DEBART (Descartes et les Mathématiques) à propos de carrés et triangles équilatéraux (deux "CarTriEq", nom barbare que j'ai donné à cette paire). je pense cette fois que les liens entre Penta15 et d'autres figures est bien établi. Certains résultats ont été utilisés dans certaines des figures suivantes (indépendamment, mais cela montre bien leur rôle)

Dans le même ordre d'idée : une autre approche de Penta15 comme hexagone particulier ayant 5 côtés sur 6 isométriques, et avec utilisation de paires "carré-triangle équilatéral"(CarTriEq) toujours sur le thème carrés-triangles équilatéraux avec un Penta15 qui serait l'enveloppe minimale convexe d'un assemblage de CarTriEq

Rosace de Diane est l'essence même d'une rosace fondée sur des carrés et triangles équilatéraux autour d'un hexagone régulier. La paire carré/triangle équilatéral, que j'ai appelée CarTriEq, est une forte association créatrice. Le site "Descartes et les Mathématiques" est riche en exercices qui portent sur cette figure ou des figures plus complexes, mais construites autour d'elle. D'autres de mes variations sur ce thème à titre de complément.

Pierre CRESPIN	Penta15 et rosace de Diane	rosaceDiane
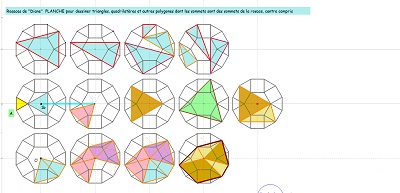
Approfondir l'étude de la rosace "de Diane" , qui cachait bien le quinzième pentagone pavant le plan, découvert en 2015 (les propriétés de cette rosace sont déterminantes pour celles du pavé "Penta15" et pour tous les pavages abordés). Enfin compléter l'étude de la paire "CarTriEq", assemblage d'un carré et d'un triangle équilatéral avec côtés isométriques, ainsi que celles d'autres figures utilisant un ou des carrés et un ou des triangles équilatéraux.
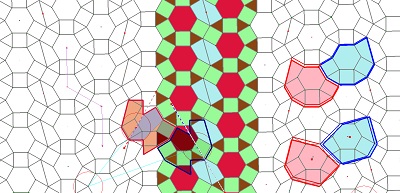
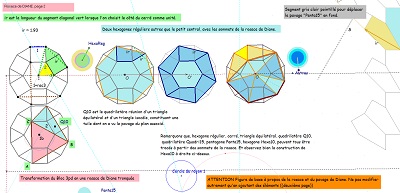
J'ai adopté le qualificatif de rosace de Diane, comme d'autres auteurs l'ont fait avant moi, pour désigner le dodécagone régulier, bien classique, pavé par des carrés et des triangles équilatéraux de côtés isométriques et dont le pavage du plan, bien classique lui aussi, comporte des rosaces qui s'assemblent en superposant un carré et deux triangles, pavage qui est un pavage archimédien de type (3.4.6.4) (Tangente n° 6 d'août 1988!) et que j'ai aussi qualifié de "islamique" en référence à "Islamic Patterns" de Keith Critchlow où il est présenté comme tel. 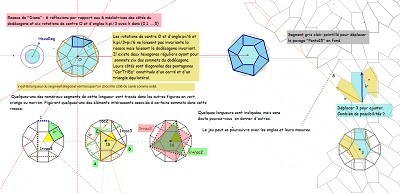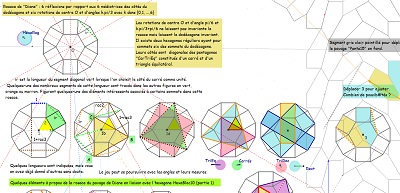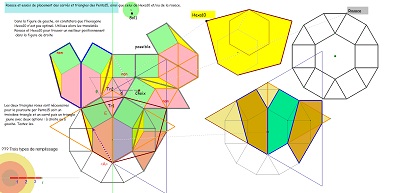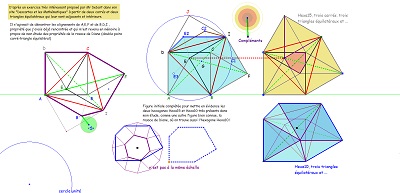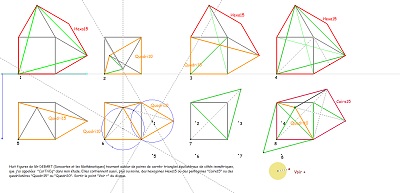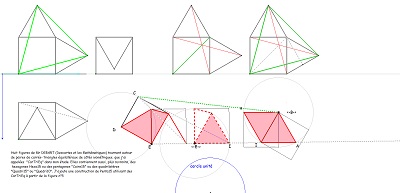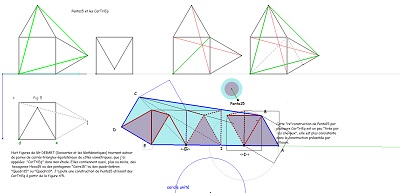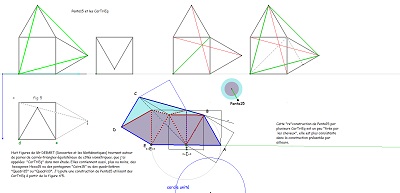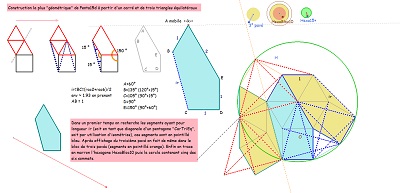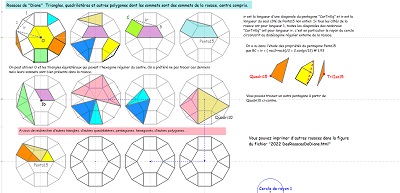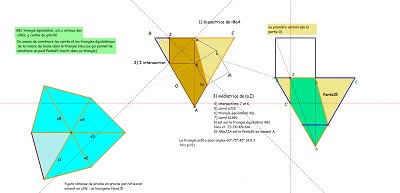Comme pour l'étude du pentagone "Penta15", je continue à prendre pour unité de longueur le côté commun des carrés et triangles équilatéraux, et ce lorsque rien ne s'y oppose ; ceci conduisant à affirmer qu'alors la diagonale du pentagone "CarTriEq" a une mesure irrationnelle égale au nombre que j'ai nommé "ir" valant 2.cos(pi/12) soit (rac2+ rac6)/2 #~1.93. Nombreux sont les segments de ce type dans la rosace de Diane et rappelons que c'est aussi la mesure du seul côté du pavé Penta15 autre que 1 ou 2, toujours avec la condition du choix fait de l'unité de longueur. En l'absence d'indication contraire, c'est ce choix qui est sous-entendu. Les premières figures ci-dessous doivent éclaircir ces remarques
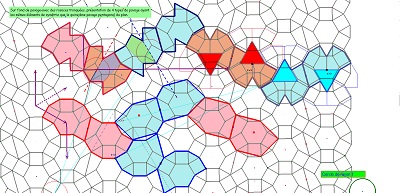
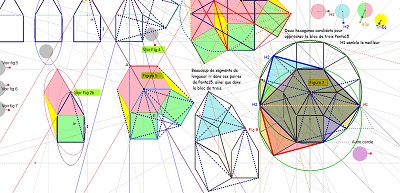
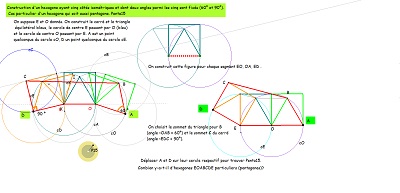
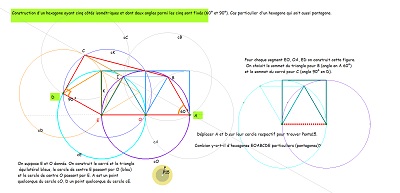
Les figures suivantes sont destinées à justifier à la fois que le pavé Penta15 était un bon candidat à paver le plan et que la rosace de Diane y est pour quelque chose. Et que l'étude un peu plus approfondie de la rosace de Diane donne quelques preuves de la cohérence avec le quinzième pavage pentagonal du plan. En s'intéressant à certains segments ayant la même longueur, on fera la découverte d'un hexagone, présent dans la figure, à deux côtés "équipollents" (donc pavant le plan), dont cinq côtés sont parmi les segments précédents, donc isométriques, mais aussi la découverte d'autres "figures" polygonales ou assemblages de polygones rencontrées dans notre étude..
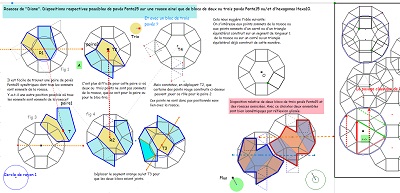
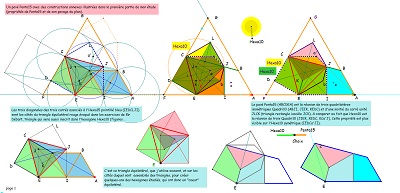
	la considération d'une paire de pavés Penta15 nous conduit à l'introduction d'une rosace de Diane ...
	... ou plutôt de l'une ou l'autre de deux rosaces.
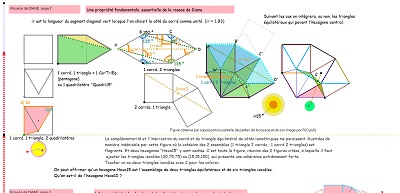
on reconnait aussi l'hexagone Hexa10 ... et son pavage par des triangles vus par ailleurs
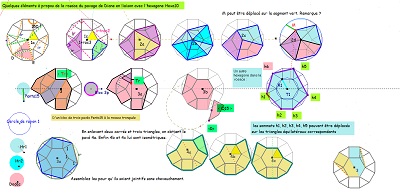
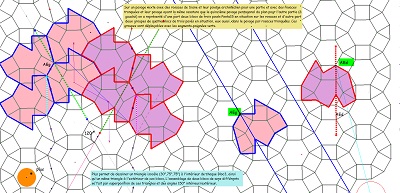
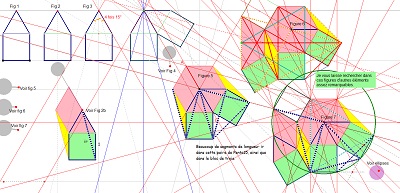
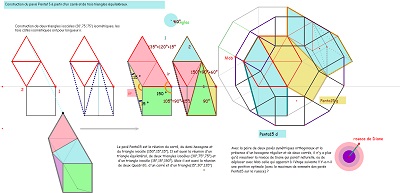
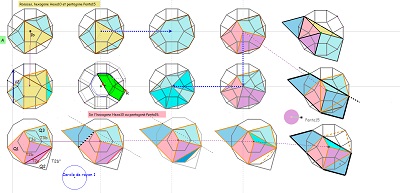
toujours en travaux et à reprendre	Première fois où apparait un pavé Penta15 (grand) dans une rosace de Diane dont une couronne est obtenue par symétries successives de blocs de trois pavés Penta15. ^^
Cette rosace de Diane est bien la figure par laquelle il aurait fallu commencer ! Le bloc de trois pavés Penta15 s'adapte assez bien à elle et l'hexagone Hexa10 a tous ses sommets qui en sont aussi sommets, il en est donc un sous-ensemble. Une paire de pavés Penta15, visibles si l'on trace deux segments "diagonaux", "de travers",! et même un trio de pavés ... ainsi que des pavés divers rencontrés dans cette étude se trouvent bien présents (voir aussi les figures ci-dessous).
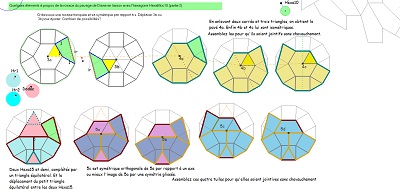
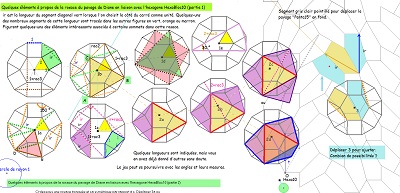
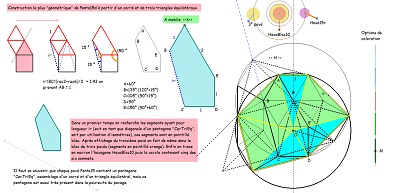
Découverte de nombreux éléments d'une assez grande diversité (ou peut-on parler de richesse ?) en cours de modification


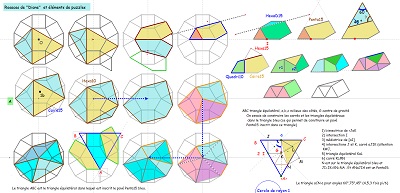
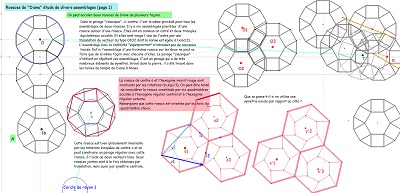
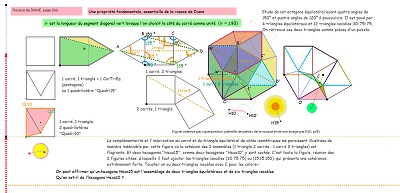
avec divers puzzles de Penta15 ^^	le triangle (45,60,75) et l'hexagone Hexa15	un Penta15 de plus, mais plus grand que celui (vert) naturellement présent dans la rosace. ^^
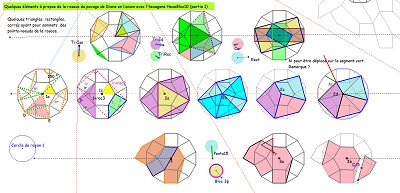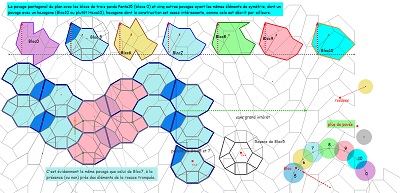
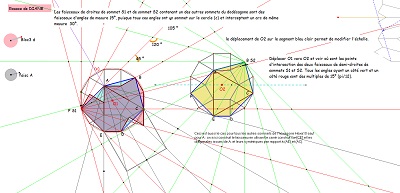
	Où la rosace de Diane et Hexa10 expliquent mieux la présence multiple d'angles 15° dans un bloc de trois Penta15 ---- >>.
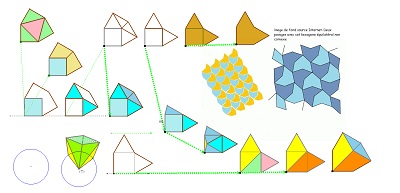
	d'autres éléments pour Hexa15 et un autre hexagone,sur fond d'une figure vue sur internet (hexagone non convexe pavant le plan et bien présent dans la rosace de Diane)
	2022 RosaceDiane3.html	PavagePenta15 2021 RosaceNew1.html

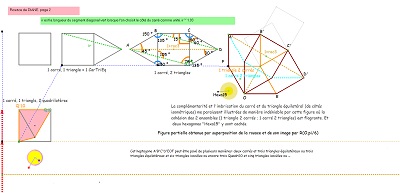
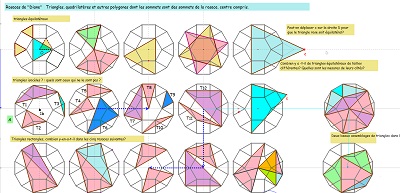
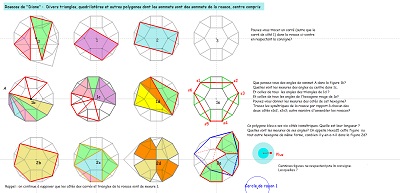
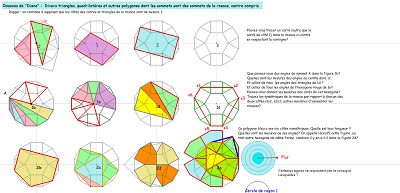
Parmi les figures dont les sommets sont des noeuds de la rosace, centre compris, (19 points) , il y a nombre de triangles, nombre de quadrilatères, au moins deux pentagones Penta15, des hexagones divers dont des réguliers, un dodécagone régulier, etc...
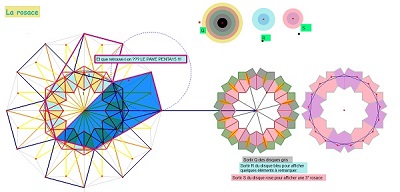
RosaceDeDiane.html	RosacesDeDiane7.html
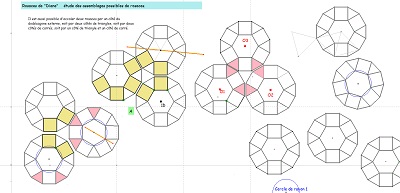
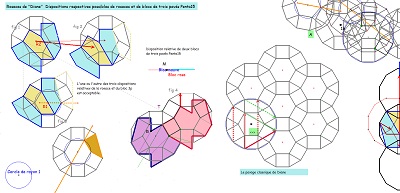
^^ Rosaces et pentagones Penta15		Pour imprimer une page de rosaces de Diane^^

Assemblages possibles de rosaces de Diane ou de rosaces issues de rosaces de Diane dont des rosaces "tronquées"
On a été amené souvent à choisir un mode d'assemblage pour des blocs ou pour les rosaces étudiées. On essaie de faire le point sur les divers cas rencontrés pour les rosaces de Diane, mais aussi pour d'autres tuiles comme les rosaces tronquées, dont la présence a été assez naturelle dans certains cas (ou pour des parties de ces rosaces).


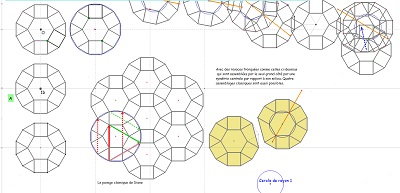
Pour tester la meilleure position relative d'un des deux blocs de 3 Penta15, de l'Hexa10 et de la rosace support ---- >> à revoir quel intérêt ici ??

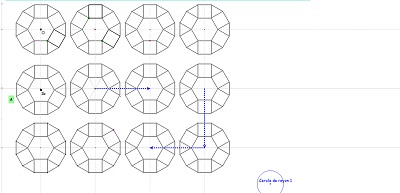
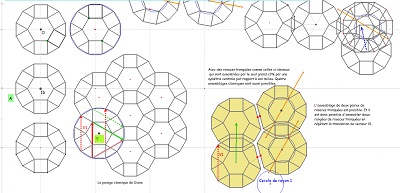
Dispositions relatives de rosaces et de blocs de trois pavés avec assemblage de deux blocs symétriques orthogonaux. Blocs déjà évoqués, comparés à la rosace la plus adaptée

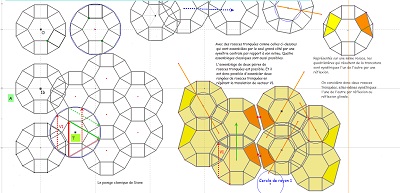
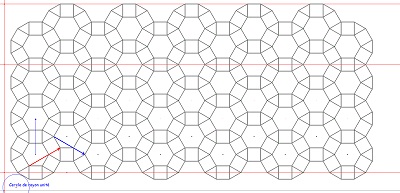
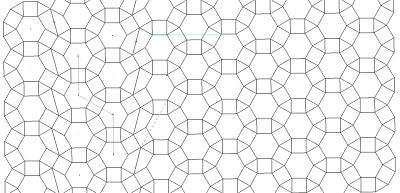
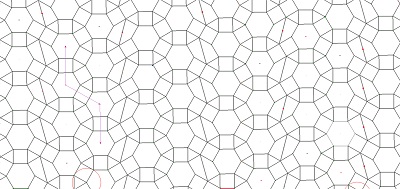
pavage rosaces de Diane v	pavage avec les deux pour comparaison	pavage rosaces de Diane tronquées v

suite (PavageRosaces10.html)	suite Puzzles15.html	Retour Compléments en vrac
Sommaire Partie II	Sommaire 2020 Penta15	sommaire Penta15

PLUS : Supplément à propos de Carré-triangle équilatéral (CarTriEq)
En prolongement de figures très intéressantes du site de Patrice DEBART (Descartes et les Mathématiques) à propos de carrés et triangles équilatéraux (deux "CarTriEq", nom barbare que j'ai donné à cette paire). je pense cette fois que les liens entre Penta15 et d'autres figures est bien établi. Certains résultats ont été utilisés dans certaines des figures suivantes (indépendamment, mais cela montre bien leur rôle)

Dans le même ordre d'idée : une autre approche de Penta15 comme hexagone particulier ayant 5 côtés sur 6 isométriques, et avec utilisation de paires "carré-triangle équilatéral"(CarTriEq) toujours sur le thème carrés-triangles équilatéraux avec un Penta15 qui serait l'enveloppe minimale convexe d'un assemblage de CarTriEq



Rosace de Diane est l'essence même d'une rosace fondée sur des carrés et triangles équilatéraux autour d'un hexagone régulier. La paire carré/triangle équilatéral, que j'ai appelée CarTriEq, est une forte association créatrice. Le site "Descartes et les Mathématiques" est riche en exercices qui portent sur cette figure ou des figures plus complexes, mais construites autour d'elle. D'autres de mes variations sur ce thème à titre de complément.