Pierre Crespin
Propriétés du Bloc10/Hexa10, hexagone pavant le plan
PavageHexa10.html

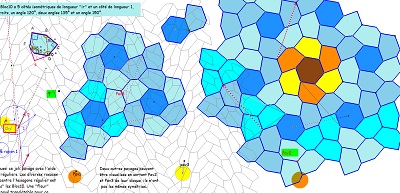
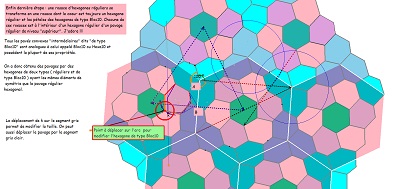
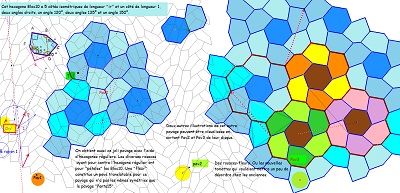
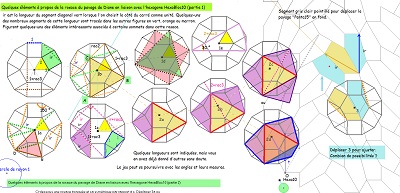
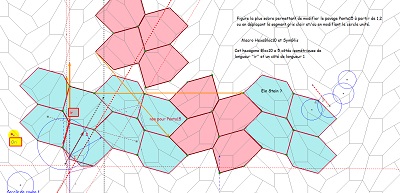
Le dernier pavé-bloc (hexagone Bloc10 ou encore Hexa10 par la suite) ayant deux côtés "équipollents" est donc un hexagone pavant le plan (condition suffisante à voir auprès de Thérèse Eveilleau et Pierre Jullien). Deux des pavages du plan s'obtiennent à partir d'un pavé par symétries centrales et translations, mais il permet aussi plusieurs autres pavages différents, dont celui qui a les mêmes éléments de symétrie que le pavage "Penta15" comme nous l'avons déjà évoqué; et même une infinité en incluant ou supprimant ou non des paires de colonnes bleu ou rose en n'oubliant pas l'utilisation possible de l'autre face du pavé
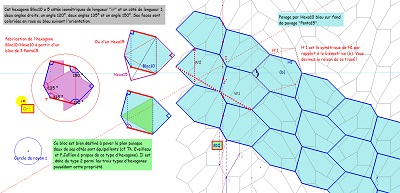
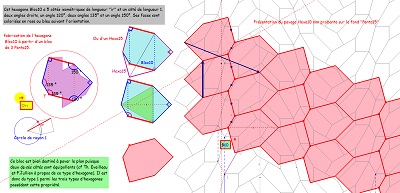
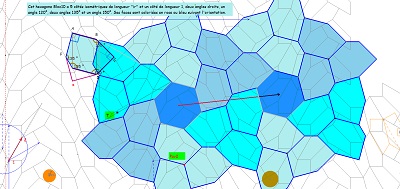
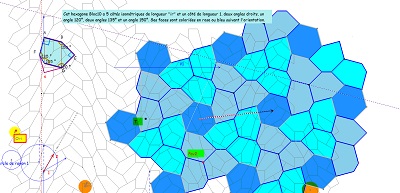
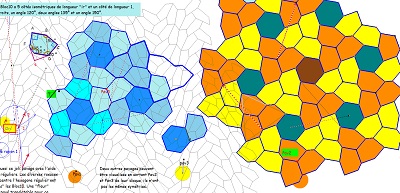
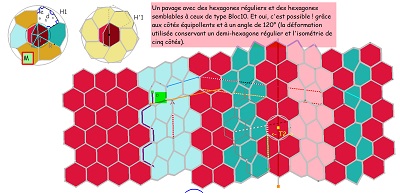
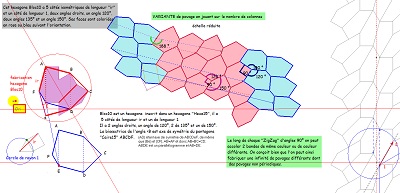
Ci-contre les deux pavages réguliers/périodiques (avec une seule face utilisée) et leurs éléments de symétrie , mais c'est un pavage mixte qu'il nous faut élaborer.

Le pavage du plan avec Hexa10 ayant les mêmes éléments de symétrie que le quinzième pavage pentagonal . Il est constitué par l'assemblage dans les angles droits en alternance de paires de deux colonnes de pavés de même orientation.

 

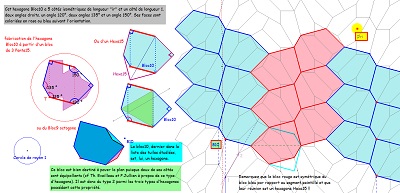
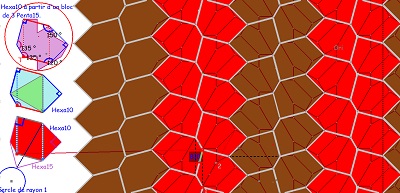
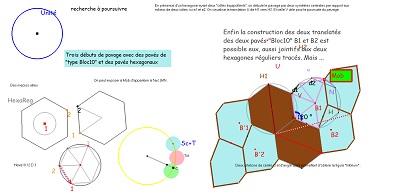
et une justification supplémentaire sur fond de pavage "Penta15", après remarque d'une propriété importante de ces hexagones Hexa10.

Hexa10PavageChoixTexte.html
Ci-dessous : un autre aspect de la modification possible en remplaçant les colonnes bleu par deux colonnes rouge (ou l'inverse) ou encore en modifiant le nombre de colonnes, Il est aussi possible d'inclure une ou des colonnes de pavés carrés; mais le pavage perd la propriété d'avoir les mêmes éléments de symétries que le pavage "Penta15".

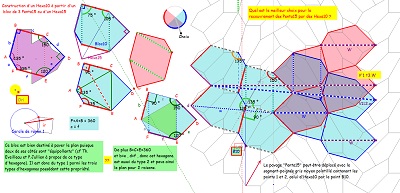
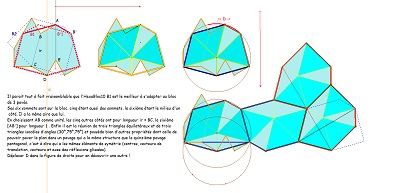
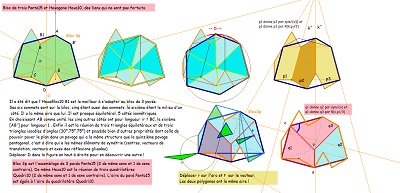
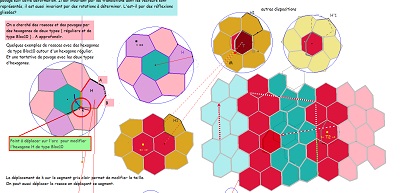
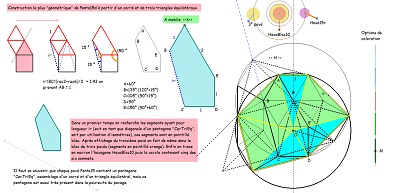
Quelques propriétés de cet hexagone côté angles et comparaison à Hexa01 (déjà évoqué, dont il emprunte une moitié pour l'accoler à un quadrilatère Quadri15)
et à Hexa15 dont il est aussi issu assez naturellement.
Retour sur une figure où je ne l'ai pas vu (à l'époque) à partir d'un bloc de trois pavés Penta15 ! En ajoutant le cercle contenant 5 des 6 sommets, beaucoup d'égalités d'angles deviennent évidentes. Ainsi que le dodécagone inscrit dans ce cercle.
et comparaison avec d'autres polygones de l'étude
Parmi les propriétés intéressantes de cet hexagone (hexagone Hexa10) :
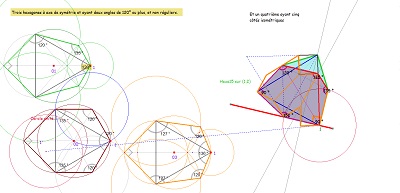
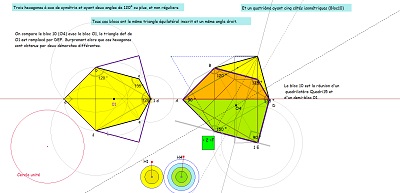
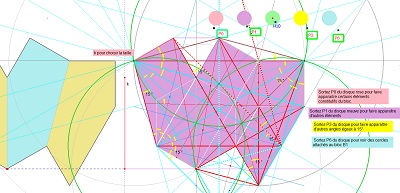
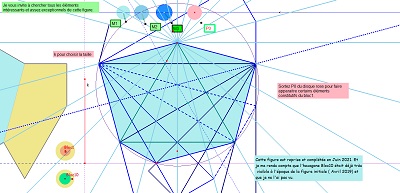
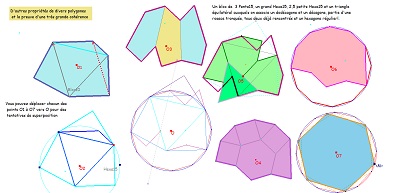
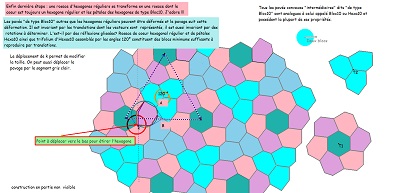
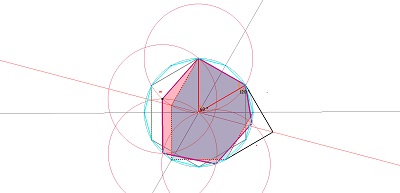
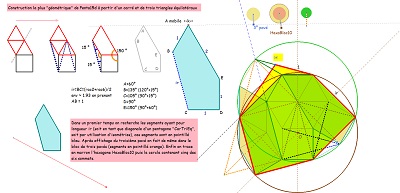
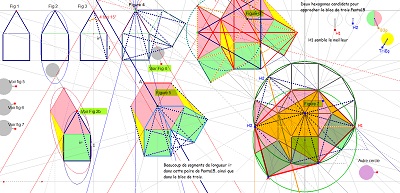
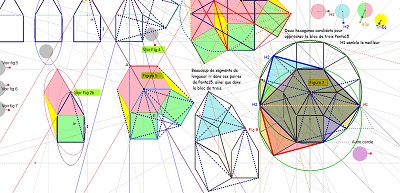
il est obtenu aussi par déformation d'un hexagone régulier en conservant l'isométrie de cinq des six côtés, ... et cette déformation a un certain effet sur un carrelage de tomettes. Dans cette déformation on appellera hexagone "de type Bloc10" les éléments de la famille d'hexagones aux diverses étapes de la transformation.
Complément Déformation (HexagonesReguliersDeformes)
Ces déformations m'ont été inspirées par les études sur les pavés équilatéraux évoquées par ailleurs, en ayant pour objectif l'isométrie de 5 des 6 côtés (soit un hexagone "presque équilatéral").
Ci-dessous, trois figures CABRI permettent l'animation de cette déformation (sous Cabri).
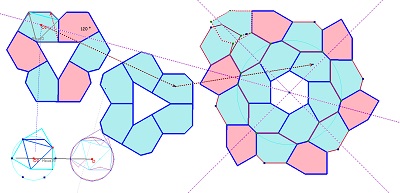
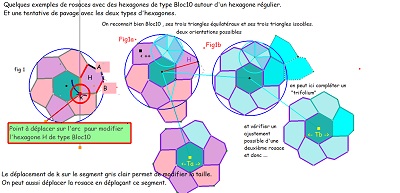
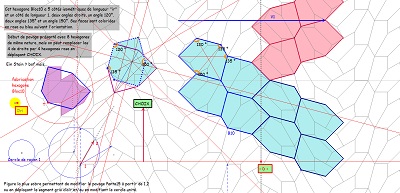
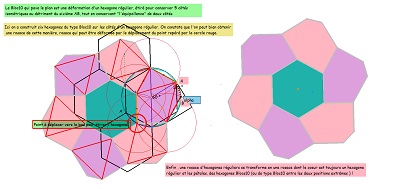
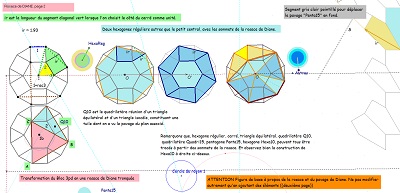
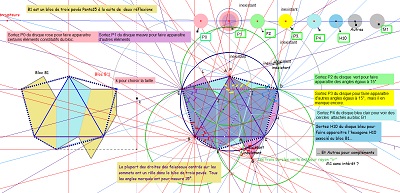
Parmi les propriétés de ces hexagones et des pavages associés figure la présence possible de rosaces "mixtes" avec leur création ci-dessous.

Divers développements ci-dessous à base de ces rosaces et d'un trifolium intéressant.
Variantes de pavages avec l'hexagone Hexa10 ou de "type Bloc10"et des hexagones réguliers ou des triangles équilatéraux.
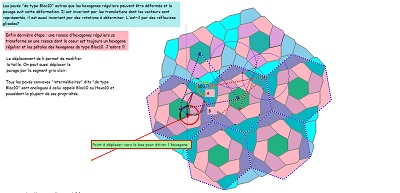
Deux rosaces et des trifoliums isométriques, puis poursuite cohérente créant un ou des pavages périodiques avec l'aide d'hexagones réguliers.
Il en est de même des Hexa "de type Bloc10" en ce qui concerne cette dernière propriété.
On a mis en évidence une structure hexagonale auto-similaire (?) fractale (?) Outre le pavage du plan, déjà vu, ayant les mêmes éléments de symétrie que le pavage pentagonal par Penta15, on obtient un pavage avec l'hexagone Hexa10 (ou avec l'hexagone de "type Bloc10") et l'aide complémentaire d'hexagones réguliers ... centres de rosaces, avec début, ainsi, d'un autre pavage périodique du plan.
variantes en complément avec des pavés de type Bloc10

chacune des "rosaces-fleurs" est un pavé qui pave le plan avec une structure triangulaire ou/et hexagonale! On peut aussi faire apparaitre les trifoliums plutôt que les rosaces, ou les deux.
et en intercalant des trifoliums ...
en poursuivant sur ce thème, il est possible de faire se cotoyer des rangées de tomettes régulières et des rangées de tomettes "Hexa10 ou de type Bloc 10", ou des rangées de tomettes de deux types "Bloc10", toujours avec un paramètre non contraint pour Bloc10, et donc avec une assez grande liberté de panachage, la largeur de chaque colonne de tomettes hexagonales étant aussi un élément non contraint.
quelques éléments en cours à titre de justification
et ici des pavages mixtes (hexagones réguliers/ hexagones déformés d'une autre façon que celle des hexagones "de type Bloc10", mais étant aussi un assemblage de six triangles (trois équilatéraux/trois 3 isocèles). On a alors l'impression de colonnes où les tomettes ont été compressées.
Ces hexagones (de "type Bloc10") se retrouvent, me semble-t-il, dans le site de Jaap Scherphuis dans une image animée concernant les hexagones convexes. A vérifier (c'est fait, c'est bien le cas). Ma propre étude en est indépendante. Il serait intéressant de confronter les deux approches.
 

Et une nouvelle tentative pour évaluer la cohérence de tout cela. Je me rends compte que certaines de mes digressions autour de rosaces, de blocs de trois pavés sont ici de retour, avec cette rosace du pavage de Diane (que je n'ai pas assez explorée et exploitée ).
page provisoire à ce propos rosaceDiane.html
 
Non seulement la rosace de Diane contenait, cachés, plusieurs pavés Penta15, mais elle contenait aussi l'hexagone Hexa10et d'autres éléments rencontrés dans cette étude; la symétrie exemplaire de la rosace a-t-elle interdit de tracer un trait de travers entre deux sommets? une diagonale ? On a vu précédemment que la structure du pavage "Penta15" est assez semblable à un pavage "islamique" , lui-même issu du pavage des rosaces de Diane.
On remarquera que, sous réserve du choix du côté des carrés de Penta15 comme unité de longueur, un côté de l'hexagone Hexa10 a pour longueur 1, les cinq autres ont pour longueur "ir" (diagonale du pentagone carré-triangle équilatéral); c'est un peu l'inverse de la propriété du pavé Penta15 ( un côté ir, trois côtés 1, un côté 2, ou cinq côtés 1 ?).
Ces dernières figures laissent à penser que de nombreux éléments sont issus de la rosace (type pavage de Diane) et que la recherche, dans cette rosace, des segments de longueur ir, aurait mis en évidence le pavé Penta15 et l'hexagone Hexa10.
Comparaison avec d'autres hexagones construits sur un triangle équilatéral, en reprenant un peu les figures précédentes. HexagonesRencontres
Complément Déformation (HexagonesReguliersDeformes)
ComplémentsEnAttente

Sommaire Partie II ou Sommaire 2020 Penta15 ou sommaire Penta15
Conclusion P2