Pierre CRESPIN
Etude sur le quinzième pavage pentagonal du plan
Quelques autres nouvelles figures en attente (ComplementsEnVrac).
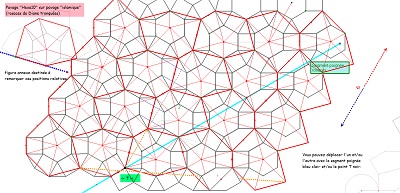
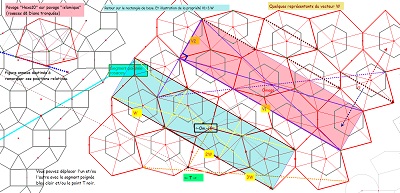
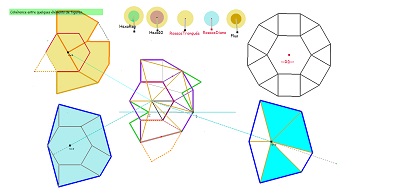
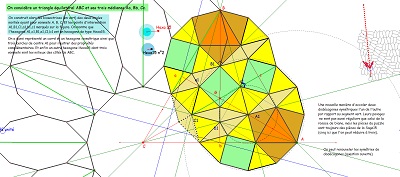
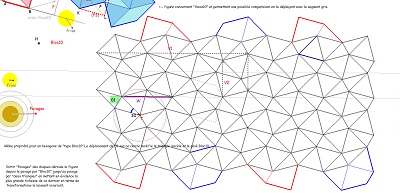
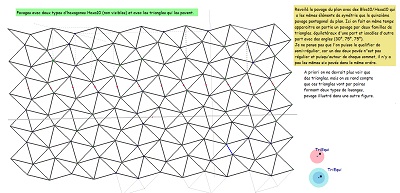
Hexas10, rosaces de Diane tronquées, et interprétation des vecteurs de base des translations laissant le pavage invariant et de la relation V1=3W.
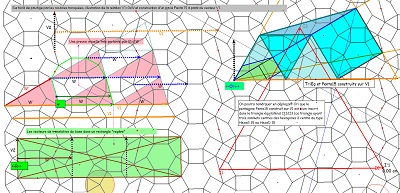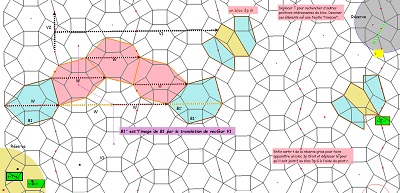
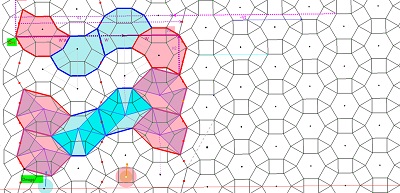
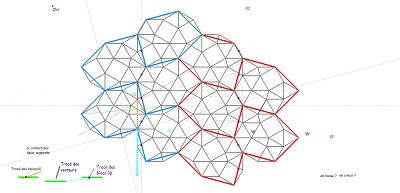
Retour sur les positionnements relatifs des pavés ou blocs de pavés et des rosaces tronquées (ou non) et sur fond de pavage par les rosaces tronquées
des figures reprises et/ou complétées    

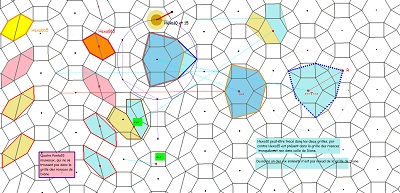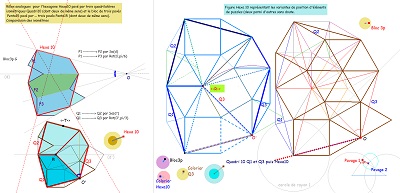
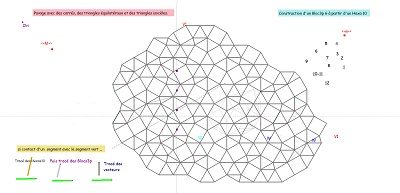
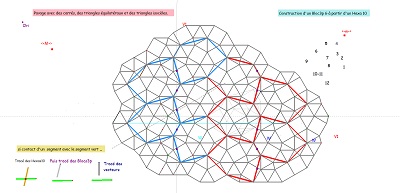
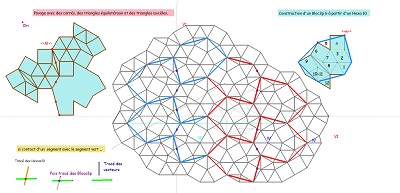
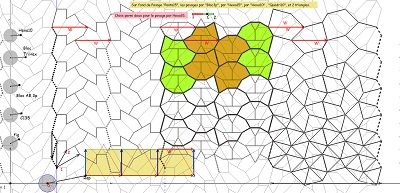
Sur fond mixte de rosaces, deux ensembles de quatre tuiles à déplacer pour comparer les tentatives de positionnement. Voir aussi l'interprétation de la relation V1=3.W avec figuration des W comme vecteurs liés aux blocs "coquilles" et aux hexagones Hexa10, aux blocs de trois Penta15 ou aux rosaces tronquées..

 
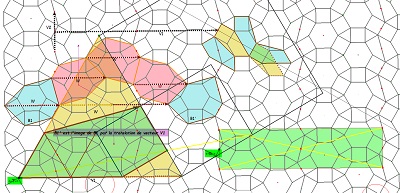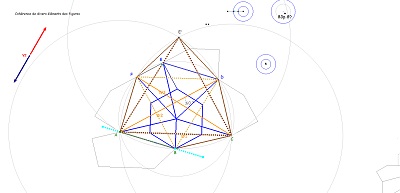
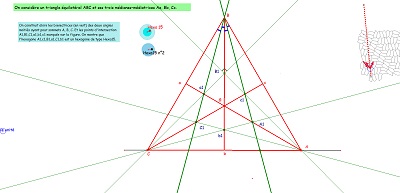
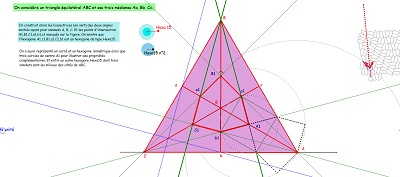
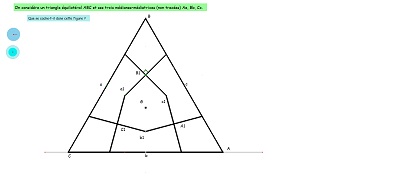
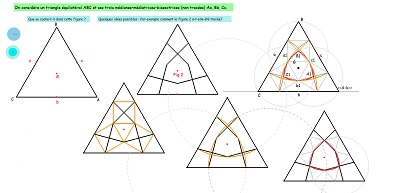
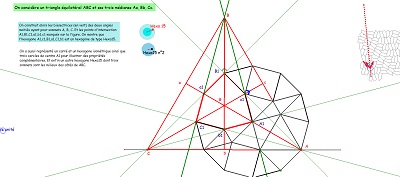
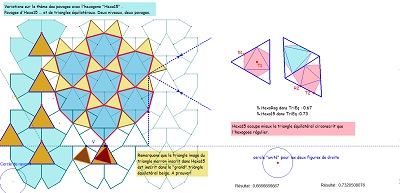
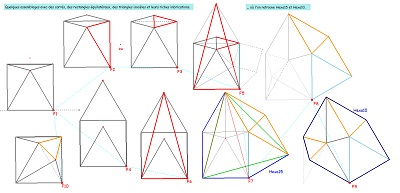
Une jolie propriété des "quadri-sectrices" du triangle équilatéral, qui fait pendant au fait qu'un hexagone Hexa15 a deux triangles équilatéraux inscrits, obtenus en joignant les sommets un sur deux (vu par ailleurs). Hexa15 et triangles équilatéraux sont très liés, imbriqués, l'un n'allant pas sans l'autre.
Triangles équilatéraux, carrés et hexagones Hexa15 font partie de cette "Saga15" que j'ai déjà souvent évoquée autour de Penta15.

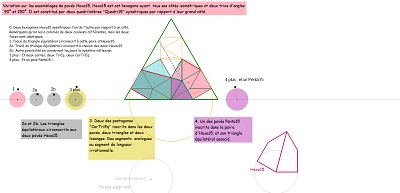
deux, puis des, Hexa15 dans un triangle équilatéral

à revoir objectif pas clair
 
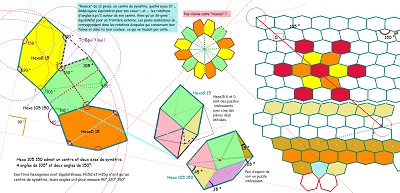
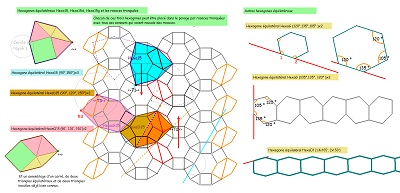
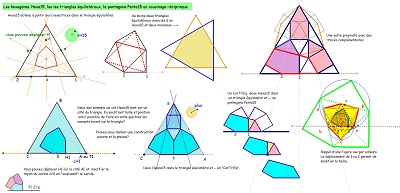
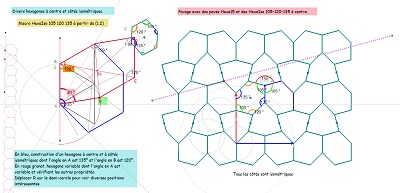
Les hexagonnes Hexa15, HexaD15, HexaG15 pavent le plan à l'aide de triangles équilatéraux, ou non. En cmplément pour Hexa15 : Voir quelques figures comme celles ci-dessous dans les pages TechniquesSuperpositions et AutresPavages2
un exemple assez intéressant de reconnaissance de motifs sur une image de pavage (utilisée en fond de figure Cabri) dont je ne retrouve pas l'origine. Merci à son auteur de me permettre de l'utiliser.
<<--- Pavages par carrés et triangles équilatéraux en lien avec Penta15.

<<-- Quelques pièces de puzzles liées au CarTriEq

Tentative de recherche de pavages avec, pour tuiles, des Penta 15 et divers éléments de la saga 15 dans des motifs de "rosaces"--->>
ComplementsEnVracPlus
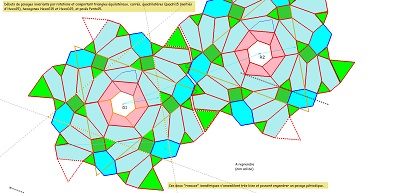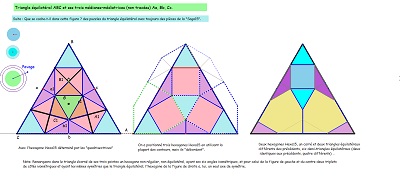
Rappel NOTE : les termes utilisés (ossature, structure, ... ayant mêmes éléments de symétrie que ...) sont un peu vagues, peut-être volontairement, en particulier parce que le pavage par Penta15 est le pavage par ce pavé pentagone (découvert en 2015) et que les autres pavages de l'étude sont des pavages par des blocs de trois pavés ou des pavages par des tuiles ayant la même aire que le bloc de trois pavés Penta15. C'est à ce niveau-là qu'il est question de structure et qu'il faut donc se placer. Néanmoins, comme l'unicité du pavage par Penta15 a été prouvée, la connaissance d'un bloc de trois, ou d'une tuile, permet de retrouver chacun des pavés du pavage par Penta15. On peut ignorer dans notre recherche, au moins momentanément, les symétries liant localement les trois pavés. Remarquons que, assez naturellement, nous avons été conduits à une trisection des tuiles par des domaines isométriques (deux de même sens et un de sens contraire) obtenant ainsi localement une tuile qui est auusi la réunion de trois domaines isométriques.


Références :
J'avais affirmé au début de mon étude n'avoir pu consulter beaucoup de documents sur le sujet en dehors de ceux que je citais. Je n'étais pas encore bien rompu à ces recherches. Après quelques mois (années?) passés, il me semble avoir pu consulter de nombreux documents intéressants en liaison avec les pavages, dont les pavages pentagonaux ou/et hexagonaux. Cette liste est présentée ici : bibliographie . Et la consultation très fréquente de "Pinterest" permet aussi d'accéder à de nombreux documents de présentations professionnelles sur les carrelages, en suivant aussi l'évolution de la mode dans ce domaine. Enfin sur le plan éducatif on constate là encore qu'il existe de nombreux jeux utilisant des pavages ( à l'école maternelle ou primaire essentiellement où la pédagogie liée à la manipulation de pièces de bois pour des puzzles semble être dominante, mais aussi en collèges et lycées(?) avec de nombreux exercices ou manipulations par des logiciels de géométrie dynamique)).
J'ai pu constater que deux ou trois des éléments auxquels je me suis intéressé figurent dans les travaux consultés et sont antérieurs à mon étude, mais j'y étais parvenu indépendamment. Et cela me confirme dans mon analyse que le sujet est riche, y compris à un niveau assez élémentaire. Les emprunts ou prolongements sont à priori indiqués. Merci de me contacter en cas de problème.

suite et presque fin (TousLesPavages)
Conclusion Partie2
Sommaire Partie 2 ou Sommaire 2020 Penta15 ou sommaire Penta15
Bibliographie
mais aussi ...
Rapide présentation de l'étude sur "Orange"
Résumé en 10-15 figures
Résumé en 45-50 figures
sommaire Penta15 (étude complète)
Toujours en cours de mise au point
? diaporamas (chez Google ou avec Powerpoint)
 

SUITE en attente de suppresssion.
Retour sur la paire Carré-Triangle équilatéral ("CarTriEq" , nom barbare que j'ai donné à cette paire et à qui j'attribue un rôle prépondérant dans l'étude)
En prolongement de figures très intéressantes du site de Mr DEBART (Descartes et les Mathématiques) à propos de carrés et triangles équilatéraux (deux "CarTriEq" donc ). je pense cette fois que les liens entre Penta15 et d'autres figures qui en découlent est bien établi.
Dans le même ordre d'idée : une autre approche de Penta15 comme hexagone particulier ayant 5 côtés sur 6 isométriques, et avec utilisation de paires "carré-triangle équilatéral"
toujours sur le thème carrés-triangles équilatéraux
avec un Penta15 qui serait l'enveloppe convexe d'un assemblage de CarTriEq
 
Compléments DeuxTrianglesPropriétés
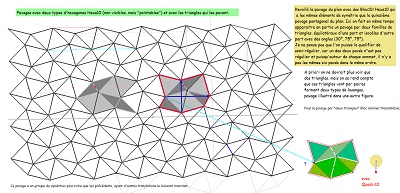
Retour sur les choix possibles dans la formation du pavage par Hexa10
Et une bonne raison à partir des pavages par des triangles équilatéraux et triangles isocèles
en constatant qu'un espoir de plus de périodicité est incité par un changement de sens
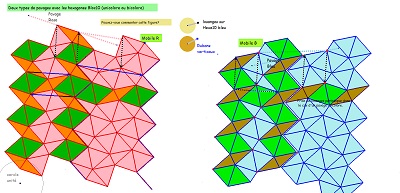
Rubans de losanges dans les pavages unicolores
et dans le pavage bicolore ci-dessous ! ( mieux )
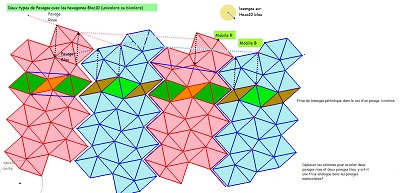
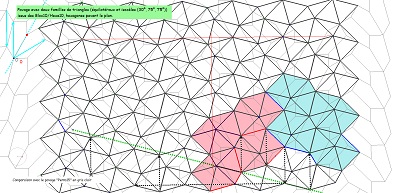
Illustration de l'existence d'une translation qui laisse des frises invariantes dans le pavage "deux triangles" issu du pavage par Hexa10/Bloc10 ayant mêmes éléments de symétrie que le pavage Penta15 (pavage bicolore par les Hexa10). Comparaison pavage "deux triangles", pavage "Penta15".
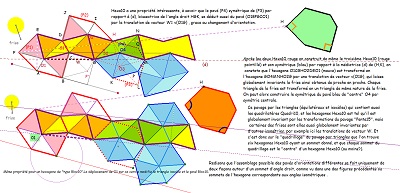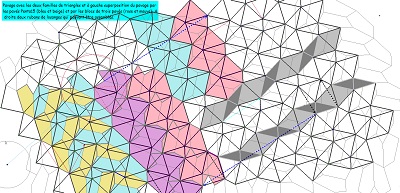
Ces dernières figures explicitent plus nettement le pourquoi des diverses impressions émises à propos d'un multiple pavage par les pavés Hexa10 ou de "type Bloc10". Si l'on "efface" les hexagones Hexa10 ou Bloc10 qui ont conduit au pavage par les "deux triangles", il est possible, sur le "quadrillage-maillage triangulaire", de trouver plusieurs hexagones Hexa10 (Bloc10) ayant un centre donné, et plusieurs (six) hexagones Hexa10 (Bloc10) ayant un sommet donné. Rappelons aussi que chaque noeud du maillage est l'extrémité de six segments dont cinq sont isométriques, ce point est donc le centre d'un cercle contenant cinq sommets.
 
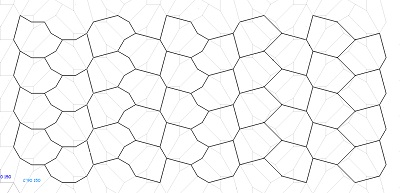
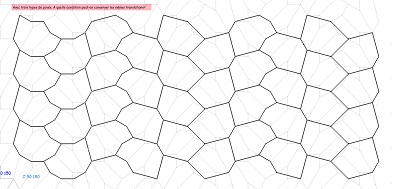
De nouveaux projets de découpe pour puzzles ...
 
dimensions à revoir pour que toutes les images soient à la même échelle. A reprendre
 
en cours... Puzzles15.html