Pierre CRESPIN
Etude sur le quinzième pavage pentagonal du plan
HexagonesRencontres
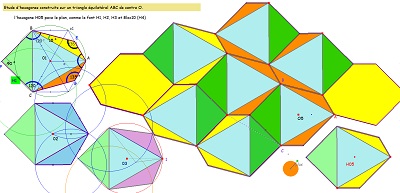
l'hexagone Hexa10 et d'autres hexagones analogues
Sommaire Partie II
     

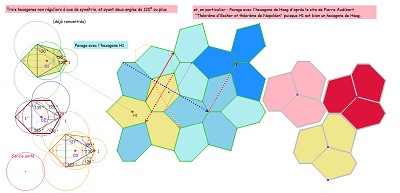
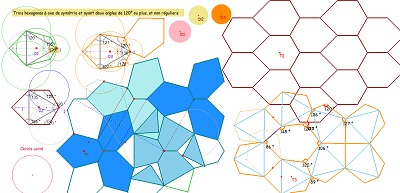
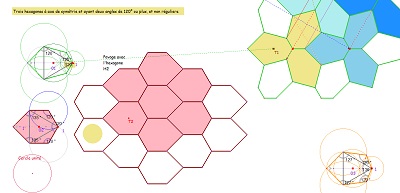
Il existe 3 types d'hexagones pouvant éventuellement paver le plan. Les sites sur le sujet parmi ceux consultés :
-Thérèse Eveilleau et Pierre Jullien pour les hexagones ayant deux côtés "équipollents", condition suffisante pour paver le plan dans "Mathématiques Magiques".
- Pierre Audibert, Michaël de Villiers pour les hexagones de Haag s'appuyant sur les triangles équilatéraux et trois rotations d'angle -2pi/3,
ainsi que celui de Mr Denez (figures, figure de pavage et photo de pavés en ciment)

... et mes variations sur leurs études. J'ai choisi, pour l'essentiel, des triangles ayant un angle parmi 90, 105, 120, 135, 150°, mais les hexagones ne sont pas tous du type "pavant le plan"
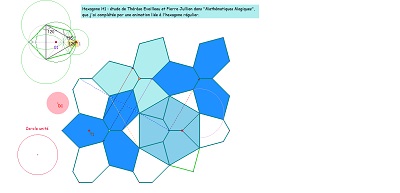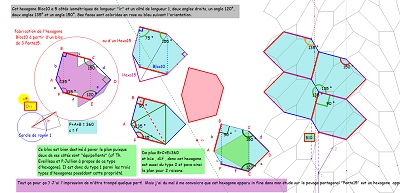
Cet hexagone nommé ici H01 est un de ceux présentés dans "Mathématiques Magiques". Remarquons que les "trifoliums" sont déformés d'un hexagone régulier.
Pavages à partir de ces hexagones ?
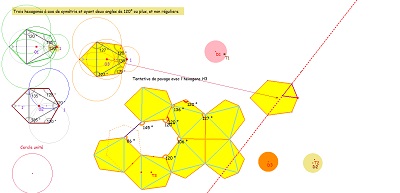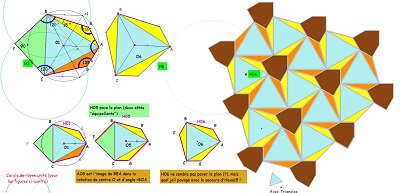
Illustration de la construction d'un hexagone de Haag et mode d'assemblage des tuiles à partir du travail de Pierre Audibert (lien très intéressant, doc .pdf)

 
D'autres divagations sur des hexagones !
  
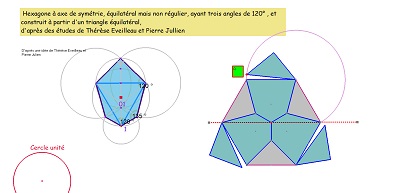
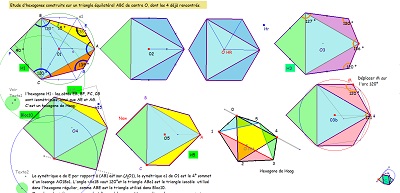
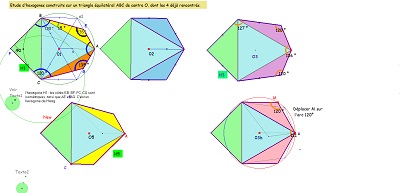
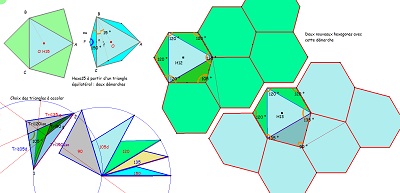
Etude d'hexagones obtenus par assemblage de triangles autour du triangle équilatéral, comparaisons intéressantes.
Examiner les assemblages possibles, comme celui donnant l'hexagone H05 à deux côtés "équipollents".

Hexag03 v
Hexag05 v
Hexa04 est Bloc10 v
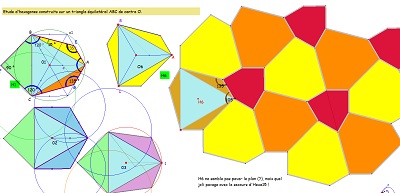
quelques pistes ou débuts de pistes
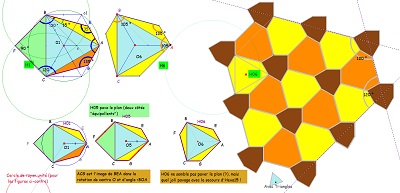
Hexag06
Hexag06
Hexag06 avec triangles équilatéraux
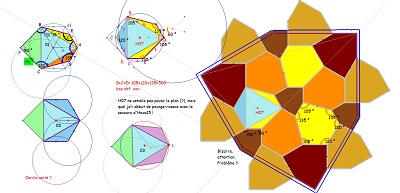
Hexag07
Hexag08 et variant plus libre
variant de Hexag08 (Hexag09)
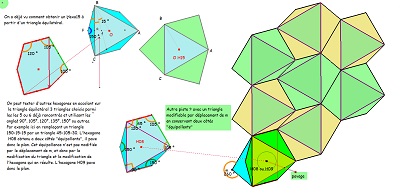
Hexag10 et Hexag11(=H02) V
Hexag12 et Hexag13 v
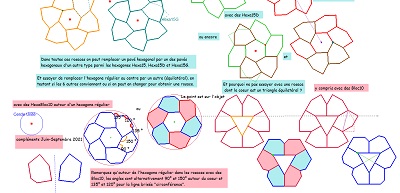
Ci-contre on a retrouvé H01 et/ou H02
d'autres assemblages à venir pour ces triangles ajustables (étude en cours à revoir)
Ces études m'ont amené à revoir certains sujets déjà abordés, par exemple comme ci-dessous,
en ajoutant de nouvelles rosaces avec la tuile HexaBloc10 (ou plus simplement Hexa10) ou avec la tuile "de type Bloc10" (qui sont aussi à rajouter à la fratrie "Penta15")
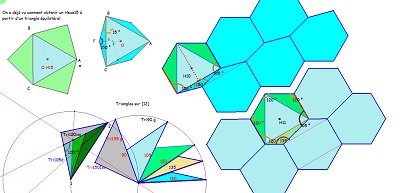
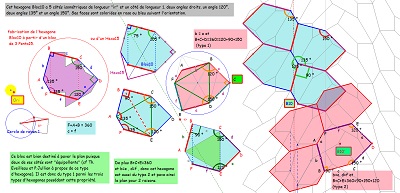
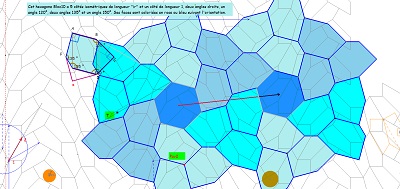
Au moins deux types de pavages pour Hexa10 ... et des rosaces d' Hexas10 autour d'hexagones réguliers avec des symétries de rotation d'ordre 6.
A voir aussi pour Hexa06 et Hexa07.
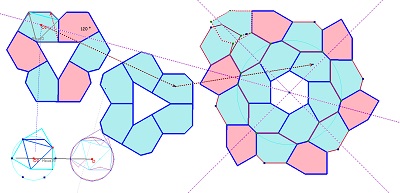
Et des pavés déformés à partir des hexagones réguliers
ComplémentsEnVrac

Sommaire Partie II ou Sommaire 2020 Penta15 ou sommaire Penta15
ou vers Conclusion Partie II