avec des compléments sur Hexa15 et des hexagones rencontrés au fur et à mesure ou rencontrés sur d'autres sites
Nouvel hexagone que l'on rend équilatéral,.
... mais il y en a d'autres
hexagones à centre avec un angle de 120°
Autres hexagones avec un axe
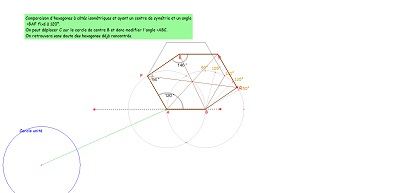
le nouveau pavage associé et la comparaison à tous les hexagones à centre ayant un angle de 120° (dont l'hexagone régulier et ceux étudiés auparavant)
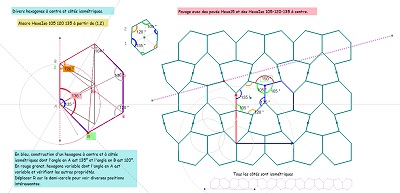
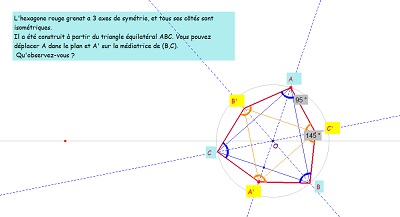
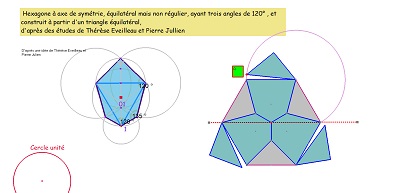
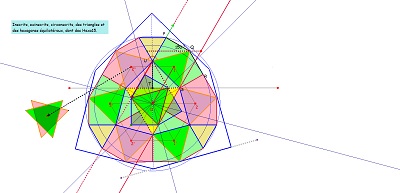
un hexagone dont trois sommets forment un triangle équilatéral et ayant trois axes de symétrie comme Hexa15.
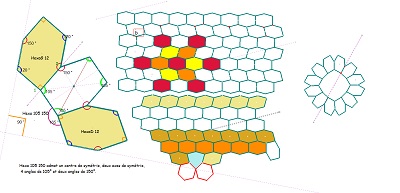
Quand trois hexagones en étoile forment une tomette
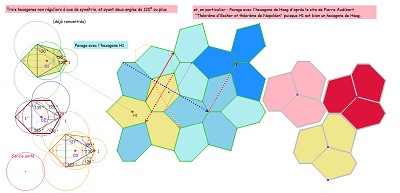
Hexa15 est assez intéressant, on l'a déjà vu, voici encore quelques commentaires et propriétés diverses qui le confirment.
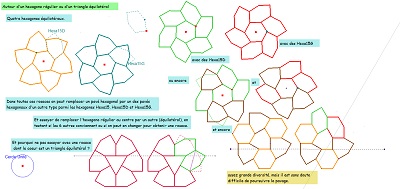
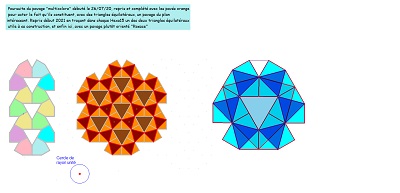
Fleurs et rosaces
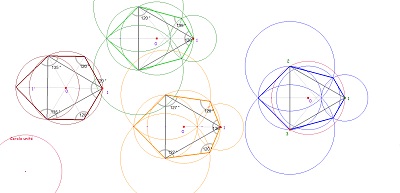
Hexagones Hexa15 et triangles équilatéraux inscrits ou "circonscrits"
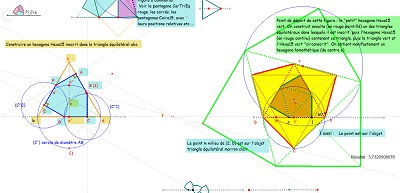
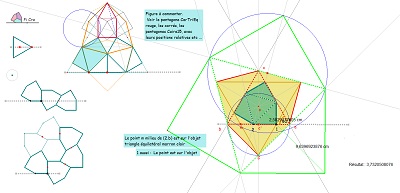
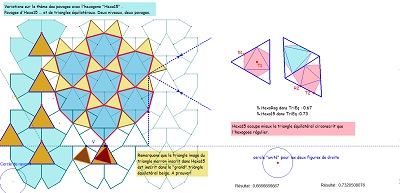
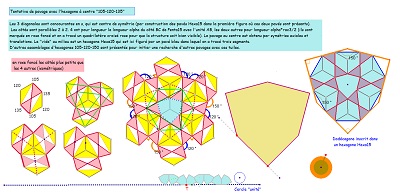
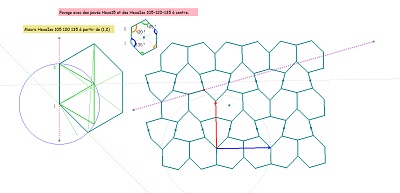
Un pavage "surprenant" par un hexagone"105-120-135", où on retrouve un pavé Hexa15 au centre, et un pavé Hexa15 "circonscrit" à la rosace extraite à droite.
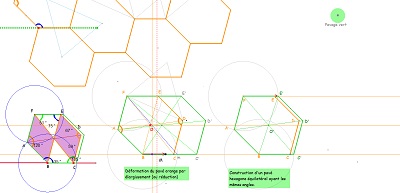
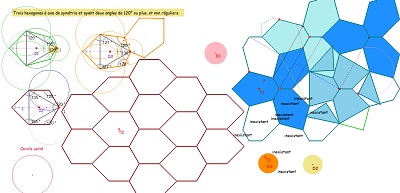
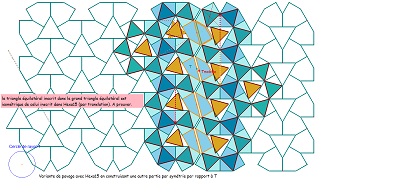
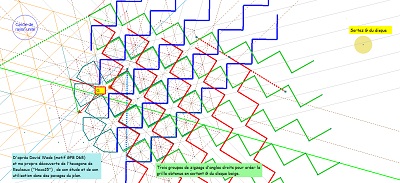
Ci-dessous variations sur les pavages par Hexa15 d'après David Wales (seule référence trouvée sur Internet à cet hexagone Hexa15).
Site très complet sur l'étude des structures du type "pavage islamique" (à voir).
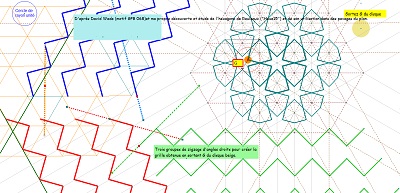
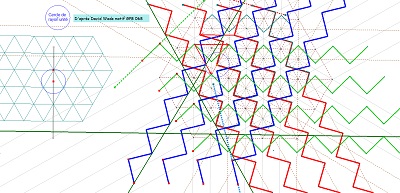
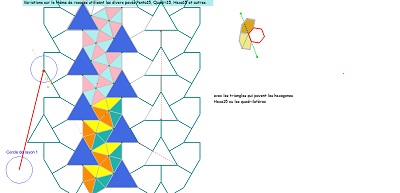
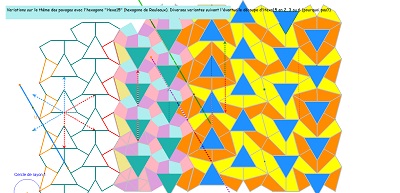
Variantes avec des pavages variés d'Hexa15 par des Quadri15, ou autres parties isométriques dont il est constitué.
Globalement les éléments de symétrie sont inchangés. Mais la multiplicité des partages possibles d'un Hexa15 crée une multitude de pavages non périodiques.
Globalement les éléments de symétrie sont inchangés. Mais la multiplicité des partages possibles d'un Hexa15 crée une multitude de pavages non périodiques.
Retour Autres Figures ou sommaire Penta15 ou Sommaire 2020 Penta15
vers Conclusion