Pierre CRESPIN
Etude sur le quinzième pavage pentagonal du plan
HexagonesSurTriEqui
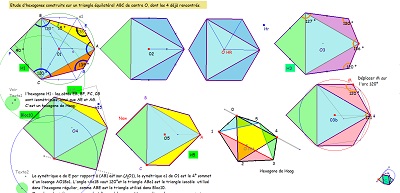
Autres hexagones analogues construits à partir d'un triangle équilatéral
Sommaire Partie II

... des hexagones déjà rencontrés et construits sur un triangle équilatéral, comparaisons intéressantes.
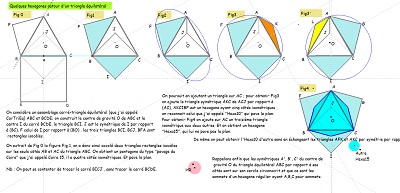
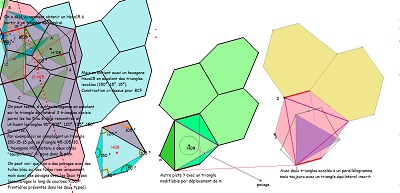
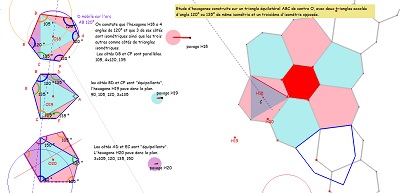
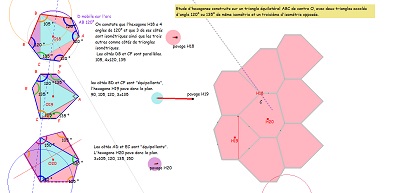
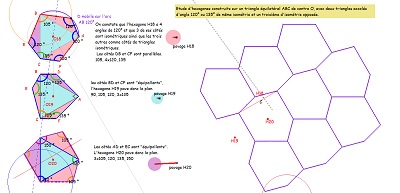
Examiner les assemblages possibles, comme celui donnant l'hexagone H05 à deux côtés "équipollents"
 

 
Quelques uns, parmi d'autres, des hexagones construits autour d'un triangle équilatéral

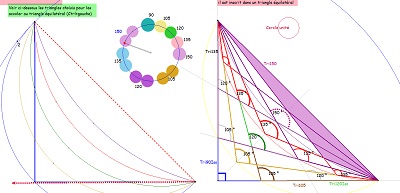
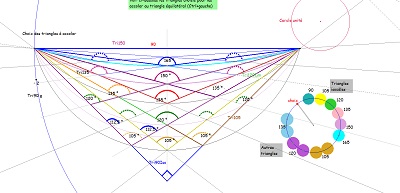
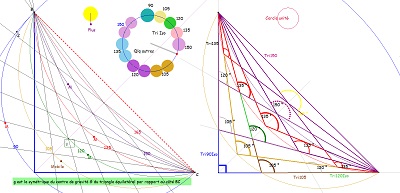
A propos des triangles à ajuster au triangle équilatéral et du choix éventuel des angles particuliers parmi 90, 105, 120, 135, 150°, voir ci-dessous le réseau des arcs "isogonaux"et des faisceaux de droites passant par les sommets du triangle rectangle isocèle.
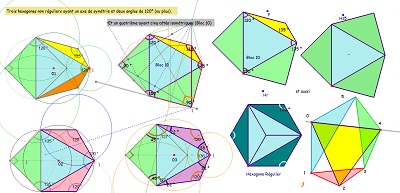
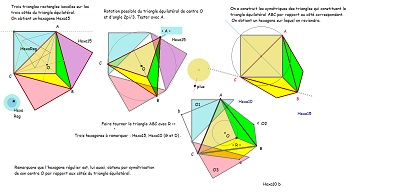
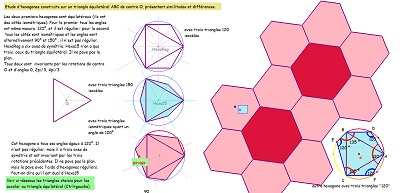
Je vois là une propriété importante de pi/12 et des angles multiples. La plupart des figures polygonales vues dans cette étude depuis le début ont des angles appartenant à la congruence de pi/12.

Bloc10 par exemple comporte tous les angles de 15° en 15° depuis 15° jusqu'à 150°
Trois hexagones particuliers plus ou moins connus. Voir aussi un quatrième à droite et plus bas sur leurs particularités.
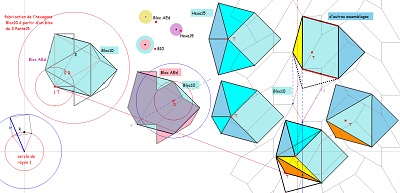
En particulier en appliquant ces ajustages pour Bloc10 ou d'autres du même type. Et avec deux côtés "équipollents" et un 3° triangle "libre"
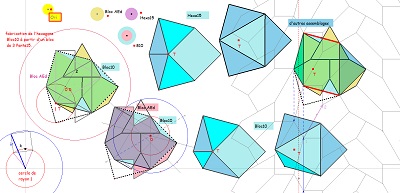
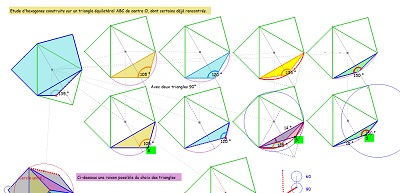
et un début d'exploration méthodique avec deux triangles rectangles isocèles  
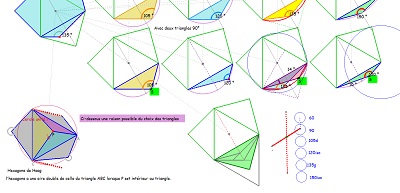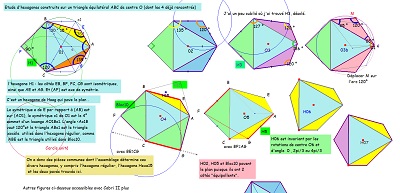
Avec ces deux triangles rectangles isocèles, on peut voir ici quel troisième triangle permet un hexagone à côtés "équipollents".
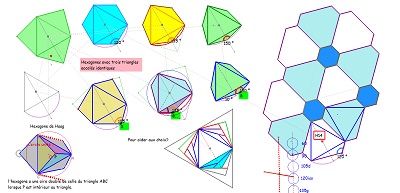
et/ou trois triangles isométriques pour d'autres hexagones
Quelques remarques
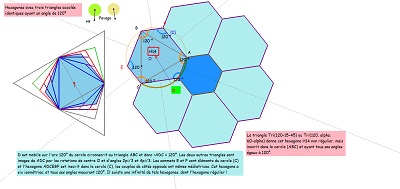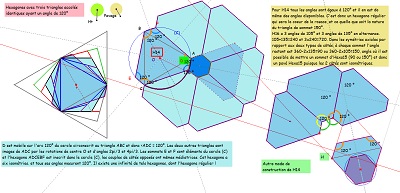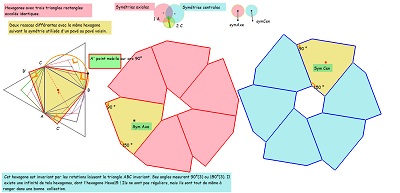
Voir sur les figures de droite les explications concernant la nature du pavé coeur de la rosace.
Et observer en détail Hexa16 (ou la variante H16b) et son(leur) pavage du plan à l'aide de pavés Hexa15.

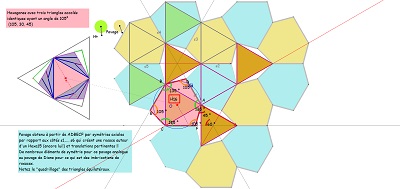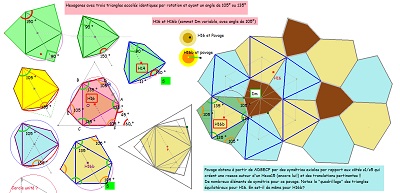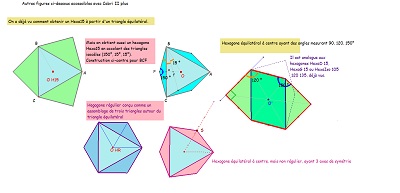
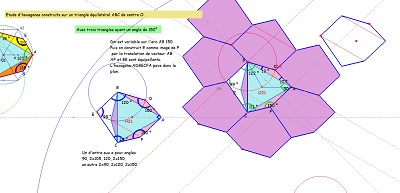
Triangles isométriques avec un d'orientation différente de celle des deux autres  

<<< --- et en cherchant un autre triangle permettant d'obtenir un hexagone pavant le plan.

Autres hexagones ayant des angles de 90° et 150° ----->>>
Et des pavés déformés à partir des hexagones réguliers ou Sommaire Partie II
D'autres assemblages pour ces triangles ajustables (étude en cours à revoir)

Retour HexagonesRencontres ou Sommaire 2020 Penta15 ou sommaire Penta15
ou vers Conclusion Partie II
ComplémentsEnVrac