ALGORITHME de construction du pavage d'un triangle d'or par des triangles d'or                                Retour SOMMAIRE                

Cet algorithme est donné dans l'article de SVM : j'en reprends en partie l'essentiel :

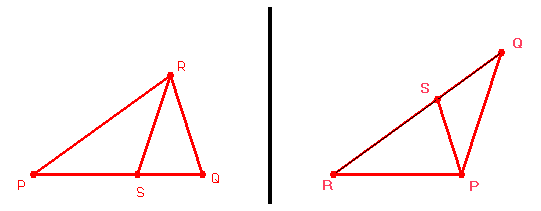
Rappel : RS est bissectrice de l'angle PRQ (figure de gauche)    et          RS = RP (figure de droite)

Suivant que le triangle à découper est de type 1 (aigu) ou de type 2 (obtus) la démarche à une étape donnée est différente.

• triangle de type 1 (figure de gauche) : déterminer le point S de (PQ) 
   (il est barycentre de (P,2-phi) et (Q,phi-1)

On obtient alors les triangles RSQ de type 1 et SPR de type 2.

• triangle de type 2 (figure de droite) : déterminer le point S de (QR)
   (il est barycentre de (Q,phi-1) et (R,2-phi))

On obtient alors les triangles RPS de type 1 et  SPQ de type 2.

On recommence, si besoin est, en respectant la règle suivante :

• A une étape on partage uniquement les triangles aigus, à l'étape suivante on partage uniquement les triangles obtus .

• Si l'on a pavé les triangles de type 1 avant cette étape, on découpera uniquement les triangles de type 2 lors de cette étape.
• Si l'on a pavé les triangles de type 2 avant cette étape, on découpera uniquement les triangles de type 1 lors de cette étape .

L'algorithme (récursif ) peut se traduire de la manière suivante :

Procédure penrose(P,Q,R,style,prof)
début
     si  prof<=1  alors tracer_le_triangle (P,Q,R)
       sinon
           si style =1 alors 
                                   début
                                      déterminer S sur [PQ]
                                      penrose(R,S,Q,1,prof-2)
                                      penrose(S,P,R,2,prof-1)
                                   fin
                          sinon

           début
               déterminer S sur [QR]
               penrose(Q,S,P,1,prof-2)
               penrose(S,R,P,2,prof-1)
           fin

fin

Voir la procédure écrite en Turbo Pascal

REMARQUE : Même si le problème de l'ordre des points est traité par l'algorithme, il est important de bien voir en quoi cet ordre est important ; aussi je complète les figures précédentes en traçant les cercles circonscrits aux triangles et en les orientant dans le sens des triplets considérés :

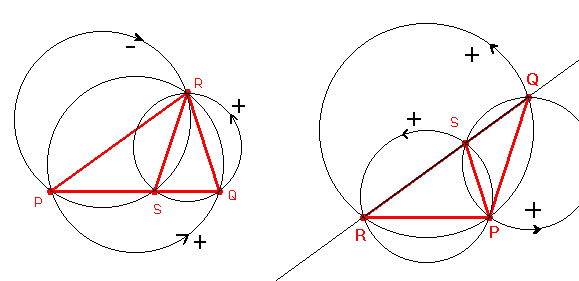
En schématisant la nature des triangles d'or par 1+, 1-, 2+, 2- on obtient :

• 1+ donne 1+ et 2-       PQR donne RSQ et SPR
• 2+ donne 1+ et 2+      PQR donne RPS et SPQ
• et par symétrie (axiale)
• 1- donne 1- et 2+
• 2- donne 1- et 2-

Voir les pages en CabriJava illustrant tout ceci (ou la page sur l'évolution du pavage, 
ou encore le diaporama sous Windows Média).

L'algorithme s'appuyant sur un ordre entre les trois sommets des triangles , il est évident qu'il existe d'autres algorithmes de pavage. Nous y reviendrons.
Enfin posons nous la question du choix de ces orientations des triangles "paveurs". Ma seule réponse à ce stade est : c'est écrit dans l'article de SVM et ... ça marche bien (!!) alors que d'autres choix (que j'ai explorés) ne conduisent pas à un pavage intéressant pour obtenir un pavage de Penrose : voir la page "autres algorithmes de pavage d'un triangle d'or avec des triangles d'or". Mais la question demeure, pour l'instant, sans réponse satisfaisante pour moi.

Quelques explications sur l'algorithme de Penrose qui s'en déduit.

Vous avez sans doute remarqué comme moi une particularité des trois cercles circonscrits dans chaque cas. Nous y reviendrons : l'idée de tracer ces cercles ( uniquement pour schématiser l'orientation du triplet dans un premier temps ) sera exploitée dans la suite.