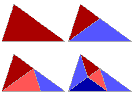
EVOLUTION du PAVAGE d'un triangle d'OR

n=0
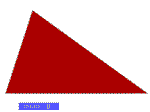
n=1
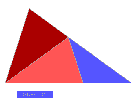
n=2	Si l'on enlève le triangle obtus de droite, on obtient alors deux triangles aigus symétriques ( vraiment puisque les orientations sont contraires ) constituant un "cerf-volant".
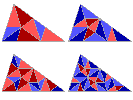
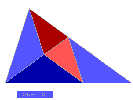
n=3	L'axe de symétrie du "cerf-volant" se confirme . De plus on voit apparaître un point important , centre du cercle inscrit au triangle aigu initial .
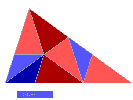
n=4	A l'intérieur du premier cerf-volant , deux "cerf-volants" plus petits se déduisent l'un de l'autre par rotation et symétrie axiale .
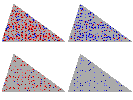
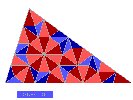
n=8	Apparition d'un décagone constitué de dix petits triangles aigus et dont le centre I est le centre du cercle inscrit au triangle initial . On peut donc paver un décagone en pavant un des triangles, puis le triangle symétrique, puis les cerf-volants obtenus par rotation d'angle 2pi/5 et de centre I. Remarquons qu'à cette étape , le triangle initial peut être presque pavé par des carreaux de deux autres types : "cerf-volants" et "flèches"
n=9	Le décagone précédent présente maintenant en son centre une étoile à cinq branches. Il est pavé par 10 triangles aigus et 10 triangles obtus ou 5 grands losanges et 5 losanges "étroits" ou encore 5 petits losanges et 5 flèches . Pour le triangle initial , le pavage par petits et grands losanges est presque possible en dehors de quelques "coupes" sur les bords ou en coin . C'est aussi le cas du pavage par flèches et losanges étroits .
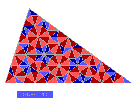
n=10	Le décagone présente maintenant 2 étoiles à cinq branches imbriquées et décalées de pi/5 et dont les cotés sont dans le rapport phi . Apparaissent deux autres décagones centrés aux points I1 et I2 centres des cercles inscrits aux triangles aigus de l'étape 2 .
n=11	Apparaissent deux pentagones , contenant le décagone de centre I et dont les cotés ont mêmes supports que 5 des cotés du décagone . On peut donc paver un pentagone avec des triangles d'or ,mais ce pavage , invariant par rotation d'angle 2pi/5 , n'admet pas pour axes les axes de symétrie du pentagone. Des décagones sont en cours de formation , ainsi que des étoiles à cinq branches .... Mais tout cela est bien normal en raison de la définition récursive,des similitudes, des symétries partielles ou des rotations qui tranforment des parties du pavage en d'autres. Remarquons que le cerf-volant de l'étape 1 semble de plus en plus posséder un deuxième axe de symétrie mais qui n'en est pas un . Cependant il semble que la partie globalement invariante par cette symétrie soit en expansion.
n=12	Les décagones ne se comptent plus (fraichement nés ou plus anciens ) : on pourrait voir leurs positions relatives : pour la plupart centrés aux sommets de pentagones réguliers dont le centre est aussi le centre d'un décagone ...

Arrêtons ici cette exploration . Vous pouvez sans doute voir d'autres propriétés intéressantes .

TOUTES LES IMAGES suivant le degré : 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15