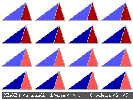
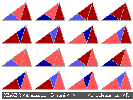
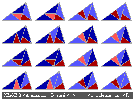
Autres algorithmes de pavage d'un triangle d'or par des triangles d'or. 

RETOUR SUR L'ALGORITHME DE PAVAGE D'UN TRIANGLE D'OR : Autres algorithmes

Revenons sur l'algorithme de construction du pavage :

PQR donne RSQ et SPR     soit 1+ donne 1+ et 2-
PQR donne RPS et SPQ      soit 2+ donne 1+ et 2+

On conçoit que, si l'on échange les deux sommets non principaux d'un des triangles obtenus, on obtiendra un algorithme différent . Et ceci, même si on gomme les différences dues à l'orientation des triangles : en effet cette orientation est déterminante pour l'application de l'algorithme.

Si l'on applique toujours la même règle à chaque étape , il y a 4 x 4 = 16 algorithmes différents pour obtenir un pavage du triangle d'or par des triangles d'or , dont 8 pour lesquels 1+ donne 1+ et 2+ ou 2-, autrement dit 8 algorithmes pour lesquels on peut conserver tout ce qui a été dit à propos de la similitude directe .
Si l'on permet de changer d'algorithme à chaque étape , mais en appliquant le même algorithme pour chaque triangle nous obtiendrons 16^n(8^n?) pavages différents du triangle à l'ordre n ou 16^Un (8^Un?), si on s'autorise à appliquer un algorithme quelconque sur chaque triangle à découper , où Un est le nombre de triangles du type concerné à cette étape.

Remarque : Je n'avais pas soulevé ce problème au moment d'exposer l'algorithme de construction , mais il était sous-jacent, par exemple dans l'application à l'aide des macro-constructions de CABRI ( choix de AIGORD ou AIGORG ). Je pense que les pavages de PENROSE ne sont pas uniquement ceux engendrés par le premier algorithme décrit longuement (voir les sites spécialisés sur ce sujet), mais ils ne le sont sûrement pas par ceux que je viens d'évoquer .

 Comparaison de l'évolution des 16 pavages suivant le degré à partir du même triangle.

avec application du même algorithme à chaque étape

Voir le diaporama sous PowerPointe

Vous pouvez remarquer que, pour un ordre donné, la densité de rouge et la densité de bleu sont les même quelque soit l'algorithme , ainsi que le nombre de triangles de chaque type. Le rapport bleu/rouge est alternativemnt proche de phi ou de 1/phi. Le nombre d'or et les suites de Fibonacci sont cachés derrière.