Retour au Menu sur les Suites en CabriJava

Retour au sommaire CabriJava

Etude de Pierre Crespin - Lycée Dumont d'Urville Février 98-Février 99

 Présentation à l'aide des logiciels CABRI II, DERIVE, EXCEL de suites récurrentes et de suites introduisant la notion de chaos déterministe.

Le point de départ de cette étude est un article de J-P Delahaye paru dans le numéro spécial "LE CHAOS" de Pour La Science et intitulé : "Le complexe surgit-il du simple ?"

Après avoir travaillé sur les "suites du chapeau de clown", j'ai pensé qu'il serait possible de présenter quelques figures CABRI permettant d'illustrer les comportement de suites récurrentes où la fonction relation de récurrence est de type affine () ou de type ou encore, pour introduire la notion de chaos, du type . Evidemment les dernières suites sur lesquelles j'ai travaillé sont les suites arithmétiques et géométriques, m'étant rendu compte que l'illustration graphique avec CABRI n'est pas sans intérêt pour ces suites élémentaires.

Dans les deux premiers cas, il s'agit de permettre des conjectures sur le comportement des suites en fonction de la valeur du U0 et des paramètres de la fonction de récurrence (variations de la suite, convergence éventuelle) et de voir que la convergence dépend de la valeur de la dérivée au voisinage du point fixe.

Suites récurrentes "quelconques": construction de Un+1 à partir de Un . Fichier : Suiteqcq.fig

Suites arithmétiques : fichier : Suitarit.fig

Suites géométriques : fichier : Suitgeom.fig

Relation affine : figure CABRI : suitaff1

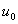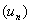Deux points B sur yy' et A permettent de modifier la relation de récurrence ( b et a). On pourra, tout d'abord, pour une relation de récurrence donnée, modifier la valeur de et voir le comportement de la suite. Puis modifier la position de B (paramètre b) et enfin la position de A (paramètre a) pour constater que la convergence de n'a pas lieu si a n'appartient pas à ]-1,1[.  Les cas particuliers a = -1 et a = 1 sont intéressants à visualiser.

Relation : figure CABRI suiterac2

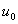Deux points B sur y'y et A sur x'x permettent de modifier la relation de récurrence et la position de la demi-parabole. On pourra tout d'abord, pour une relation de récurrence donnée, modifier la valeur de et voir le comportement de la suite 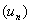; il apparaitra que pour certaines valeurs de 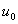la suite n'est pas définie pour tout n et qu'il est donc nécessaire de trouver un intervalle I qui soit tel que f(I) Ì I. 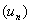Puis modifier la position de B et la position de A pour constater que la convergence de n'a pas lieu si f'(a ) n'appartient pas à ]-1,1[ où a est point fixe de f.

Relation : chargement des figures CABRI : suitepar2 , suitepar8

Suitepar2 : illustration graphique de la relation de récurrence

Suitepar8 : illustration graphique avec les premiers termes de la suite, et la possiblité de construire les courbes de f°f, f°f°f, ...etc pour expliquer certains comportements.

 Le paramètre l peut être modifié par le déplacement du sommet S de la parabole.

On pourra tout d'abord, pour une relation de récurrence donnée, modifier la valeur de 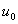et voir le comportement de la suite 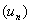. Suivant la position de S et la valeur de 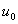on pourra observer qu'il existe des suites convergentes, des suites divergentes et éventuellement des suites périodiques. Quelques éléments des articles de "Pour la Science" sur le Chaos de Douglas Hofstadter ("L'universalité du chaos") et de Jean-Paul Delahaye ("Le complexe surgit-il du simple?") peuvent être illustrés sur les figures CABRI.

Suites du chapeau de clown : avec accès aux fichiers Excel et Derive : chaos.html

       figures CABRI clown1 , clown2

Récapitulatif : Chargement des figures CABRI :