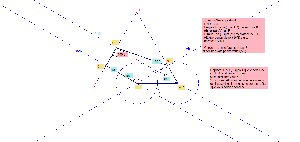


Deux étapes :
Une sécante (BC) à déplacer pour obtenir des angles convenables
puis deux sécantes et déplacer B,C,D,E pour obtenir un pavé convenable
Rappels des propriétés
Etude du pavage du plan par le pentagone Penta15
Essais de construction du pentagone Penta15
1° La construction du pentagone et les premières propriétés
- le triangle équilatéral qui le contient
-les figures simples dont il est composé
2° l'existence d'une translation potentielle pour le futur pavage.
3° Les angles du pentagone et les divers angles intervenant dans certaines figures de base comme les paires de pavés symétriques
| Une grande majorité d'angles intervenant dans la plupart des figures est constituée d'angles multiples de 15° (pi/12), les sommes aussi bien sûr (congruences modulo pi/12), mais 45°, 75° ne figurent pas dans la liste des sommes et leur présence dans un angle libre, lors d'une tentative de poursuite du pavage, signifie que le pavage ne peut se poursuivre. |
4° Les conséquences de la présence d'un seul côté de mesure irrationnelle dans les assemblages de pavés pour une poursuite du pavage.
5° Les mesures des côtés avec un choix de l'unité et les cercles de rayon 1 centrés sur les sommets.
6° une figure rassemblant la plupart des propriétés (voir la figure)
Ajoutons des essais de construction laissant un ou plusieurs degrés de liberté.
7° Des tentatives pour trouver un bon Penta15 à partir de diverses constructions
Les choix de ces figures et leur ordre de présentation sont encore à revoir
 |
 |
 |
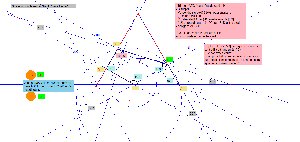
Les éléments pouvant être déplacés sont en général marqués en vert. |
RecherchePave15.html (B mobile sur (AG) |
RecherchePave15c.html (B mobile sur (AG) |
RecherchePave15_3.html (E mobile sur (AF) |
|
 |
Deux étapes : puis deux sécantes et déplacer B,C,D,E pour obtenir un pavé convenable |
||