SIMILITUDE transformant un TRIANGLE D'OR en un petit TRIANGLE D'OR, élément de son pavage.         Retour SOMMAIRE         

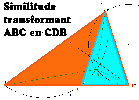  CARACTERISTIQUES de la SIMILITUDE transformant ABC en DBC :
 Montrons que O est un barycentre particulier des points A,B,C : 

En effet O est barycentre de A(a),B(b),C(c) , et comme la similitude conserve les barycentres, il est aussi barycentre de C(a),D(b),B(c) , or D est barycentre de A(1),B(phi), Considérons donc O comme le barycentre de C(a(1+phi)),D(b(1+phi)),B(c(1+phi)) et remplaçons D(b(1+phi)) par A(b) B(b.phi) .

On obtient alors O comme barycentre de A(1), B(1), C(1+phi) ou encore comme barycentre de A(1), B(1), C(1), C(phi) ou encore comme barycentre de G(3), C(phi) où G est l'isobarycentre de A,B,C. De plus O appartient à la médiane issue de C dans le triangle ABC et donc O appartient aussi à la médiane issue de D dans BCD, ce qui donne une construction géométrique simple de ce point intéressant de ces triangles ..

Ce qui est un "joli" résultat .

 Détermination géométrique de O :  On a : O est donc le point commun des "arcs capables" correspondants qu'il s'agit de déterminer .

Construire E élément de [AC] tel que AE=1 . (CD) est bissectrice de l'angle ACB , (BE) est bissectrice de l'angle ABC . I est le point d'intersection de (BE) et (CD) .

Donc O est le point commun aux arcs de cercles CIB et ADB . Le cercle (CIB) est tangent en B à (AB) et en C à (AC).

De plus : OA, OB, OC, OD forment une suite géométrique de raison 1/phi, OD, OC, OB, OA forment une suite géométrique de raison phi, et OA=OB+OC, OB=OC+OD (quatre termes consécutifs d'une suite de Fibonacci)

Remarque : Cette similitude est associée au triangle ABC et au triangle CDB . Il existe une deuxième similitude directe associée au triangle ABC : celle qui transforme ABC en BCE.