IMAGES de PAVAGES de PENROSE
Voici quelques images obtenues à l'aide de programmes Turbo-Pascal :
Un pavage d'un triangle d'or avec des triangles d'or :
Un pavage du plan avec des triangles d'or .
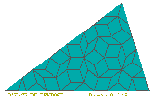Un pavage d'un triangle d'or par des losanges d'or - ou du moins presque un pavage , car il y a des "coupes" sur les bords !
Un pavage du plan par des losanges d'or .
Où l'on retrouve les triangles d'or semblables avant qu'ils ne soient eux-mêmes pavés .
Imaginez que vous partiez du petit triangle d'or ( rouge foncé au centre) et que vous appliquiez la similitude S, réciproque de celle évoquée plus haut. S tranforme donc le triangle CDB en ABC. En réitérant cette similitude, vous obtenez une spirale de triangles de plus en plus grands : on peut donc recouvrir ainsi n'importe quel point du plan par un triangle d'or obtenu par un nombre fini d'applications de S ... .
Et comme ce grand triangle peut être pavé par des petits ..., vous obtenez un pavage de Penrose d'une partie du plan , où apparaissent les triangles d'or semblables évoqués plus haut ... avec leurs pavages.
Cette dernière image illustre qu'il est possible de paver tout le plan par des triangles d'or.
Enfin l' image ci-contre met en évidence une des propriétés remarquables des pavages de Penrose :
dans un pavage par des losanges d'or : il existe des directions privilégiées : En gris foncé apparaissent des
rubans de losanges dont un coté a une direction donnée .
Les logiciels qui réalisent les images de ces pavages sont disponibles .
Un grand merci à SVM et à Fréderic Dardel , auteur de l'article , qui m'ont permis de reprendre un travail que j'avais laissé de coté .
Pierre CRESPIN Lycée Dumont d'Urville - Toulon et IREM de NICE - SOPHIA ANTIPOLIS .
SOMMAIRE PENROSE
Un pavage du plan avec des triangles d'or .
Un pavage d'un triangle d'or par des losanges d'or - ou du moins presque un pavage , car il y a des "coupes" sur les bords !
Un pavage du plan par des losanges d'or .
Où l'on retrouve les triangles d'or semblables avant qu'ils ne soient eux-mêmes pavés .
Imaginez que vous partiez du petit triangle d'or ( rouge foncé au centre) et que vous appliquiez la similitude S, réciproque de celle évoquée plus haut. S tranforme donc le triangle CDB en ABC. En réitérant cette similitude, vous obtenez une spirale de triangles de plus en plus grands : on peut donc recouvrir ainsi n'importe quel point du plan par un triangle d'or obtenu par un nombre fini d'applications de S ... .
Et comme ce grand triangle peut être pavé par des petits ..., vous obtenez un pavage de Penrose d'une partie du plan , où apparaissent les triangles d'or semblables évoqués plus haut ... avec leurs pavages.
Enfin l' image ci-contre met en évidence une des propriétés remarquables des pavages de Penrose :
dans un pavage par des losanges d'or : il existe des directions privilégiées : En gris foncé apparaissent des
rubans de losanges dont un coté a une direction donnée .