Un disque de centre O et de rayon 1/2 possède la propriété suivante :

Pour deux points quelconques M et N du disque la distance MN est inférieure ou égale à 1. 1 est le diamètre du disque. Ce disque peut se glisser à l'intérieur de toute bande de plan de largeur 1 et ce dans n'importe quelle position.

Ce n'est pas le cas d'un carré par exemple.

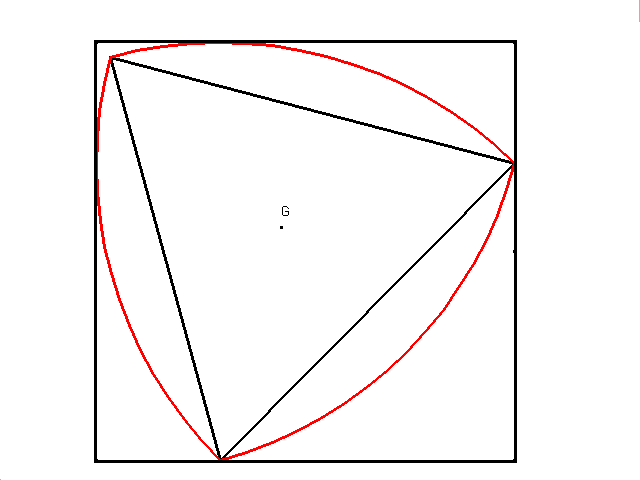
Il existe d'autres figures possédant cette propriété : exemple de ce que j'appelle "triarc" ; construit sur un triangle équilatéral, les arcs sont des arcs des cercles centrés aux sommets opposés .

 Pour deux points quelconques M et N du triarc la distance MN est inférieure ou égale à 1. 1 est le diamètre du triarc. Ce triarc peut se glisser à l'intérieur de toute bande de plan de largeur 1 et ce dans n'importe quelle position. En particulier il peut être inscrit dans un carré.

Problème :

Quel est l'ensemble des centres de gravité du triarc inscrit dans le carré ?

Figures CABRI sur ce thème :