SuitePavageOctogones

Pierre CRESPIN

Etude du pavage du plan par le quinzième pentagone

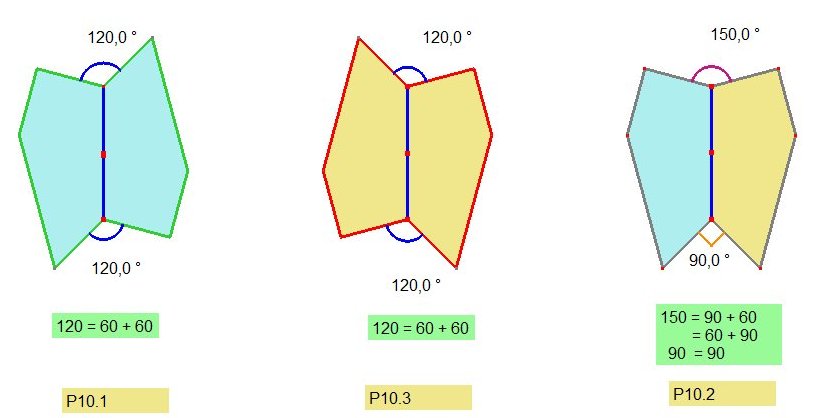
Poursuite du pavage: Nous allons partir d'une paire de pavés, mais une première considération nous conduit à choisir cette première paire de la manière suivante : le fait que le côté "BC" du pavé soit irrationnel quand les autres côtés ont pour longueur 1 et 2 fait que le côté "BC" d'un pavé ne peut être accolé qu'à un côté "BC" d'un autre pavé.	Et ceci ne peut se faire que de trois façons comme ci-dessous. Deux pavés ne peuvent être accolés par "BC" qu'en étant symétriques l'un de l'autre par une symétrie centrale de centre le milieu de (B,C) (deux premiers cas) ou par symétrie orthogonale d'axe (BC). Nous essaierons de poursuivre le pavage à partir de chacune de ces paires.
Auparavant examinons une figure préliminaire qui permettra d'exclure rapidement certains assemblages, ceci facilitant les essais de poursuite du pavage. Il s'agit de l'impossibilité d'avoir deux côtés "BC" adjacents par un sommet et ce quelque soit leur angle. Voir figure SuitePavage0New.html

Voir la figure Suitepavage1a.html pour P10.1 et P10.3 et la figure SuitePavage2.html puis SuitePavage2new1.html pour P10.2

Et de même complétons par les essais de poursuite à partir de la paire de pavés symétriques par rapport à "AE" que j'appelle paire "Coeur": SuitePavage4.html

NB : les trois figures Cabri utilisées comportent encore sans doute des erreurs ou ambiguïtés.

Avec cette étude je veux revenir sur un point qui a été soulevé à plusieurs reprises et que certaines figures étaient censées illustrer.
Il s'agit de l'unicité du pavage par le pentagone Penta 15. Pour l'instant il ne me semble pas avoir justifié correctement cette unicité.
Je pense que les figures Cabri II plug-in suivantes devraient le permettre. Vous remarquerez sans doute que, dans toutes les extensions à partir d'une paire donnée, figure assez rapidement une ou plusieurs autres paires parmi ces quatre. Et que donc il est probable que le pavage avec le pavé Penta 15 est déterminé par le pavage par ces quatre paires-octogones dont les côtés ont pour longueur 1 et 2.

Commencer par SuitePavage1.html . Elle montre que la paire P10.1 engendre un bloc unique de 6 pavés . Et qu'il en est de même du pavé P10.3 ( par symétrie axiale).

On pourra voir, avec SuitePavage1cb.html, que le deuxième bloc obtenu par symétrie axiale, peut s'accoler au premier par une rotation et une translation, mais cela n'implique rien pour l'unicité. Par contre cela confirme la possibilité de présence simultanée d'un bloc et de son image par un antidéplacemnt..

Ensuite SuitePavage3d.html permet de confirmer le choix fait et l'existence de centres de symétrie, de vecteurs de tranlations qui laissent le pavage invariant et de justifier l'unicité du pavage (à un déplacement ou anti-déplacement près).

Plusieurs étapes permettent de décomposer cette construction :

1. SuitePavage3d.html comme SuitePavage6.html permet de construire un bloc unique de 6 pavés à partir de P10.1 (paire bleue) bloc ayant encore comme centre de symétrie le point I, bloc auquel on peut ajouter un septième pavé.

2.SuitePavage3d1.html détermine à partir de ce bloc un ensemble comportant un choix possible non encore décidable entre deux solutions,

3. SuitePavage3d2.html permet de décider et de prouver l'unicité.
Et de décrire toute la construction dans une même figure Cabri. Ainsi que de présenter la figure correspondante avec ses éléments.

Enfin rappelons que nous avons déjà vu des figures permettant de montrer que les pavages "droit" et "gauche" issus de deux blocs de 3 pavés dont je me suis servi pour la construction (blocs symétriques par symétrie axiale) sont les mêmes .
Voir la page index Penta15 suite3.html (rubrique 5 du sommaire)