Pierre Crespin
Résumé en 30 figures (pentagone Penta15 et pavage)
ResumePenta15
 

Depuis le début de mon étude (il y a plus de trois ans) je tourne autour du pentagone Penta15 en cherchant en quoi il est un bon candidat à être une tuile de pavage du plan et en quoi il génère des propriétés du pavage que je trouve assez intéressantes. Je ne suis toujours pas sûr d'avoir trouvé vraiment pourquoi, bien que certaines propriétés me paraissent assez déterminantes. Ce résumé est à compléter par ceux concernant la deuxième partie de l'étude réalisée entre Décembre 2019 et Novembre 2020)

Je vais essayer de sélectionner une vingtaine de figures du pentagone Penta15 et du pavage du plan qu'il engendre, en espérant présenter l'essentiel de leurs propriétés.
 
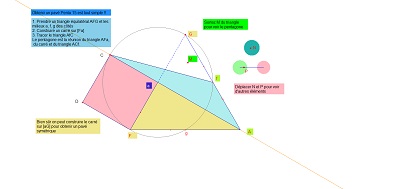
1° Présentation du pentagone, sa ou ses constructions et ses premières propriétés ( le triangle équilatéral qui le contient, les figures simples dont il est composé, ses angles,... etc)

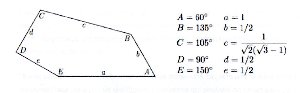
Note : pour diverses raisons souvent évoquées dans l'étude complète, j'ai choisi l'unité de telle façon que les côtés mesurent 2, 1, 2c, 1, 1 plutôt que celles notées dans la figure d'origine. Et remarquons que, alors seul un côté a une longueur irrationnelle. Tous ses angles sont des multiples de 15 °.
Des considérations simples sur quelques angles montrent que le triangle AFG dans lequel le pentagone est inscrit, a trois angles de 60°, donc qu'il est équilatéral.
Voir la figure et Voir l'image

Penta15 est inscrit dans un triangle équilatéral.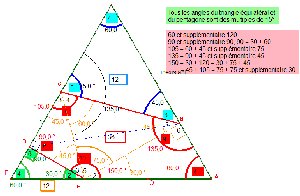
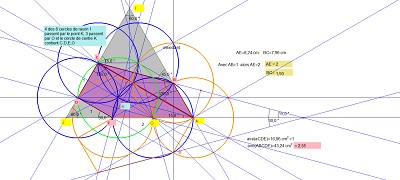On peut obtenir un pentagone Penta15 assez simplement Penta15 new >>Voir l'image
 et tous les angles liés AnglesPenta15

Construction : Pour les deux premières figures, j'ai choisi de construire le pavé Penta15 (droit ou gauche) à partir de (A,E).
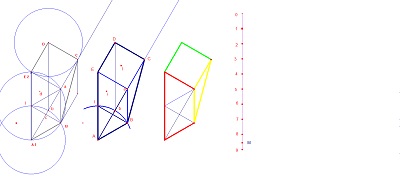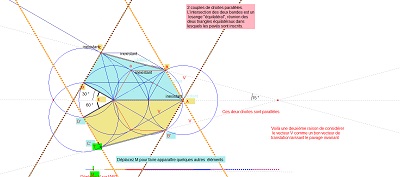
Pour la seconde on donne aussi les figures simples dont il se compose. Enfin la troisième construction reprend la construction dans un triangle équilatéral. Pour l'élaboration du pavage, d'autres constructions sont parfois nécessaires à partir d'autres côtés donnés .
Penta15 est inscrit dans un triangle équilatéral donné : figure et Voir l'image

2° l'existence d'une translation potentielle pour le futur pavage.

Possibilité d'utiliser un pavé par retournement étant donnée, voyons la figure constituée par une paire de pavés accolés par symétrie axiale, et voyons ses propriétés dans le cas de la symétrie par rapport au côté de mesure 2 et de celle par rapport au côté irrationnel. Ci-dessous à gauche.
Voir la figure

Avec le bloc de 3 pavés symétriques essayons de voir un début de construction du pavage en utilisant l'un des blocs de trois pavés . Ci-dessus à droite Voir la figure
et essai de tracé d'un pentagone inscrit dans un triangle équilatéral pour tester la possibilité de pavage. Voir la figure et la figure test
3°) Le pavage engendré et quelques images diverses obtenues en choisissant les couleurs des pavés.
pavage redressé bords épais
redressé à bords fins
New penta 719
New pavage 15n17c
 
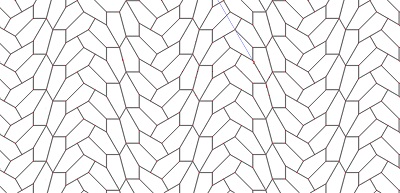
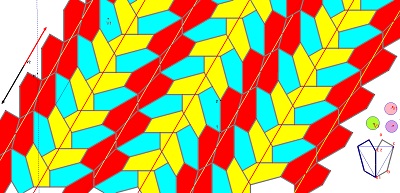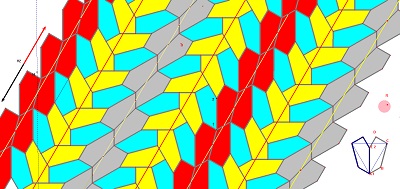
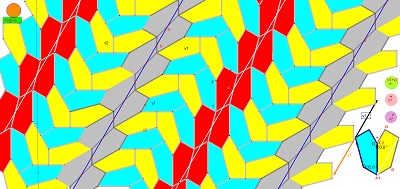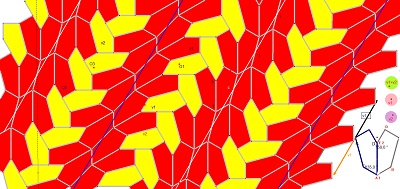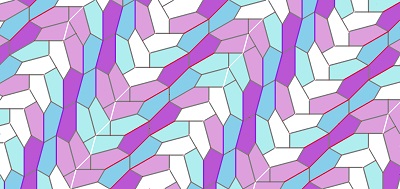Autre variante avec les directions des côtés  Penta 1511v
Penta 1522
et le pavage obtenu si on met en évidence le demi-hexagone, le carré et le triangle comme évoqué en Penta 1501a, d'abord sur les pavés "droits" puis sur tous les pavés ->
A droite une variante de pavage avec des hexagones , carrés et losanges  (et autres demi-hexagones pour boucher les trous)