Pavage du plan par le quinzième pentagone
Angle 150°

L'étude faite à propos du quinzième pavage pentagonal du plan me conduit à affirmer qu'un angle joue un rôle déterminant, c'est l'angle 150°, ainsi que l'angle 15°, mais 150 = 10x15 ! Et vous pouvez remplacer 15° et 150° par pi/12 et 10pi/12.

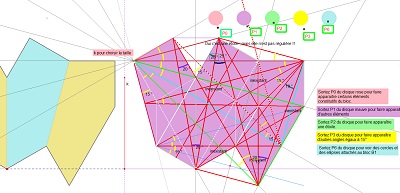
Tout d'abord rappelons que tous les angles du pavé Penta15 sont des multiples de 15° (60°, 90°, 105°, 135°, 150°), et qu'il en est de même des sommes de ces angles et des compléments à 180 ou 360°. On a vu aussi qu'il y a 10 directions de côtés dans le pavage par Penta15.
Disons aussi que 150° = 90° + 60° et donc que ce 150° apparait avec l'assemblage d'un carré et d'un triangle équilatéral, pentagone que j'ai appelé CarTriEq par commodité, qui apparait dans la construction du pavé Penta15 (et qui est déjà par ailleurs un pentagone pavant le plan).

C'est aussi ce qui a motivé l'introduction des rosaces (hexagone, carrés, triangles équilatéraux) à positionner sur le pavage "Penta15".

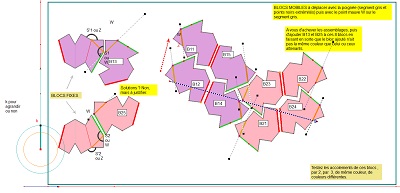
Le choix d'introduire des blocs de trois pavés a été dicté par le nécessaire assemblage de 2 pavés par symétrie axiale par rapport aux "grands" côtés, paire à laquelle il était assez naturel d'associer un troisième larron, et ce de deux façons. Ces deux blocs de 3 pavés sont symétriques orthogonaux l'un de l'autre et peuvent être assimilés aux deux faces d'un même bloc, ils ont été colorés en rose et en mauve.
De plus 3x15 = 45 , 2x45 = 90, 4x 45 =180 et 12x15 = 360. Ces blocs forment une rosace par application, de proche en proche, de symétries orthogonales.
Enfin ce bloc a deux angles de 150°, l'un saillant et l'autre rentrant, et il est là encore assez tentant de les "accoupler" par ces angles de 150°, cet assemblage est possible pour deux blocs de couleurs différentes et peut se faire de deux manières l'un par rapport à l'autre, sans qu'il y ait d'autres options d'assemblage, mais on se rend vite compte que le choix importe peu , les assemblages suivants conduisant au même état.
Pour les blocs de même couleur, l'assemblage par une translation accolant deux angles 60° (saillant/rentrant) est évident ou, sinon, par une symétrie centrale.
Les propriétés des blocs de 3 pavés (à gauche) et les assemblages de ces blocs à droite
 

Le choix de passer par l'intermédiaire de blocs de 3 pavés est un choix qui n'est valable que parce qu'il a déjà été établi, par les découvreurs, que le pavage pentagonal par Penta15 existe et est unique (à un déplacement ou antidéplacement près). Cela permet cependant de toucher du doigt ce résultat. Demeure le probléme d'existence d'autres blocs (autant que possible du type "recto-verso") qui engendrent le même pavage. Il me semble que, pour tous les blocs trouvés il y a deux angles 150° saillant/rentrant et que l'assemblage par les angles 150° est celui qui est valide pour deux blocs de natures différentes, ils se déduisent d'ailleurs l'un de l'autre par antidéplacement.
Toujours avec 150° : notez la présence des lignes brisées C 90 150 (de deux types) constituées par les côtés des angles 150° et d'angles 90°, qui sont frontières entre deux zones homogènes au même titre que les lignes brisées C135 associées aux angles 135°. Ces lignes (brisées "droites") dans le pavage du plan ont la direction globale des zones délimitées. Et on peut aussi trouver dans les rosaces des "cercles brisés" ayant aussi des angles de 150° ou 135° comme éléments constitutifs. Voir la page "lignes brisées" ici (en cours)