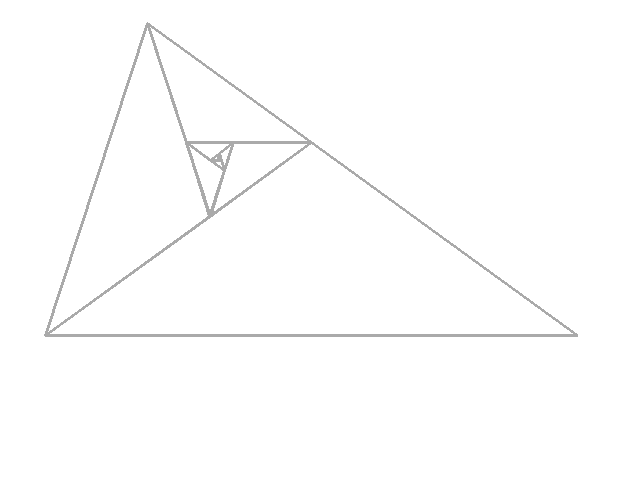
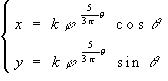Lorsque l'on construit les triangles d'or aigus déduits du petit triangle d'or par itération de la similitude S de centre W , de rapport j et d'angle 3p /5 , les sommets de ces triangles appartiennent à une spirale globalement invariante par cette similitude .
Déterminons cette spirale :
W M=r (q ) avec
et l'on a : r (q +3p /5)=j r (q )
D'où
Et sa représentation paramétrique dans un repère d'origine W :
et comme on connait les coordonnées de W dans un repère donné, il est assez facile de tracer cette spirale .
Bien sûr on est ensuite tenté de tracer non pas une spirale, mais plusieurs ou même toutes les spirales associées aux divers triangles.
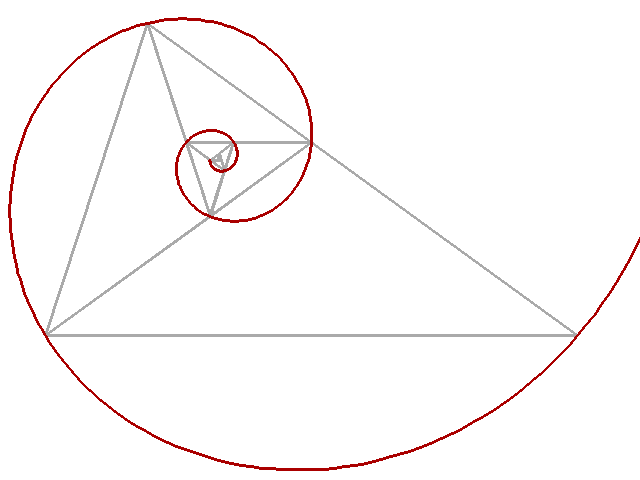
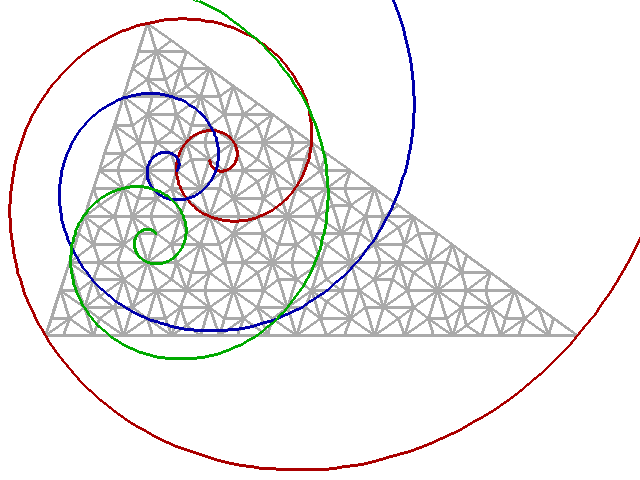
Les images suivantes montrent : les triangles d'or semblables, puis la spirale associée (en rouge), puis le pavage du grand triangle. En fin on a tiré au hasard deux triangles du pavage et l'on a dessiné les spirales associées à ces triangles en tenant compte de l'orientation ( spirales tracées en bleu et en vert ) . On s'aperçoit que ces spirales contiennent elles aussi des points noeuds du pavage, points obtenus de l'un à l'autre par déphasage de 3p /5 ou de - 3p /5 .