Penrose1b

PAVAGES DE PENROSE ET TRIANGLES D'OR

Accès à une page plus récente ( Nombre d'Or) utilisant des figures CabriJava.

NOMBRE d'OR et RECTANGLE D'OR

Est-il besoin de présenter le nombre d'or noté traditionnellement phi ( égal à (1+rac(5))/2 ) ?

Rappelons simplement qu'un rectangle d'or est un rectangle qui possède la propriété suivante :

lorsqu'on lui enlève un carré, le petit rectangle obtenu est "semblable" au rectangle initial.

Les mesures de ses cotés sont dans un rapport égal au nombre d'or phi.
Cela peut faire l'objet d'exercices intéressants, autant calculatoires que géométriques, aussi bien en Seconde, qu'en Première ou en Terminale Scientifique (avec la recherche du centre d'une des similitudes directes transformant le grand rectangle AFGD en le petit CBFG ).

Construction d'un rectangle d'or à la règle et au compas :

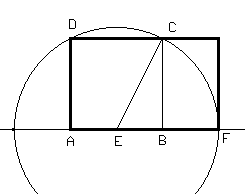
Première construction :
Construire un carré ABCD , le milieu E de [AB] et le point F de la demi-droite d'origine A contenant B tel que EF=EC . Montrer que AF= phi*AB .

Il suffit de tracer le rectangle AFGD .

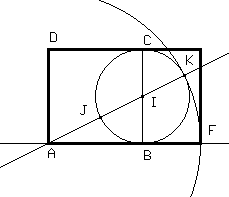
Deuxième construction :

Construire le carré ABCD , le cercle (C) de diamètre [BC] , de centre I milieu de [BC] . La droite (AI) coupe (C) en J et K ( J élément de [AI] ) . Montrer que AK = phi*AB .

La construction du rectangle d'or AFGD est alors évidente .

TRIANGLES D'OR : il en existe de deux types ( que j'appelle aigu et obtus )

Ce sont des triangles isocèles dont les cotés sont proportionnels à 1, phi, phi ( triangle aigu ) ou à 1 , 1 , phi ( triangle obtus) .
Leurs angles sont des multiples de pi/5 : pi/5 , 2pi/5 , 2pi/5 ou pi/5 , pi/5 , 3pi/5 respectivement .
Ils ont la particularité suivante : dans un triangle aigu d'or ABC de base [BC] , la bissectrice de l'angle C coupe [AB] en D tel que BCD soit un triangle d'or aigu et ACD un triangle d'or obtus ,

de même dans un triangle d'or obtus ABC de base [BC] , si D est le point de [BC] tel que BD=BA , alors ACD est un triangle d'or obtus et ABD un triangle d'or aigu :
Conséquence : on peut paver les triangles d'or par des triangles d'or !!!!

Et l'on voit se pointer les "carreaux" d'un pavage de Penrose.

Dernière remarque : ces triangles sont ceux qui interviennent dans les pentagones ou décagones réguliers.

COMMENT CONSTRUIRE CES TRIANGLES D'OR ?

Indiquons la construction pour un triangle aigu :
Le problème qui se pose tout d'abord est de savoir quel est le coté donné, ou plutôt quel est le bi-point de sommets donnés.
Supposons que le coté donné soit [OA] : ce n'est pas plus simple mais c'est de cette construction dont nous aurons besoin.
Construire le cercle de centre O contenant A , la perpendiculaire D à [OA] passant par O.

(D) coupe (C) en deux points : soit P l'un d'entre eux.
Soit O' le milieu de [OP] et (C') le cercle de diamètre [OP] .
La droite (AO') coupe (C') en B' et C' ( B'élément de [AO']).
Le cercle (C1) de centre A passant par B' coupe le cercle (C) en B et B''.
Les triangles OAB et OAB'' sont des triangles d'or aigus.
L'un est " à droite " de (OA), l'autre " à gauche ".
Sur la figure le triangle OAB est le triangle " à droite " construit sur le bi-point (O,A).
NB : la preuve est l'objet d'un exercice classique (construction d'un pentagone régulier).
Il ne reste plus qu'à définir sous CABRI la macro AIGORD en désignant O puis A comme objets initiaux et les segments [OA],[AB],[BO] comme objets finaux et sauvegarder cette macro. ( On comprend l'intérêt de créer et de sauvegarder cette macro, la construction du triangle n'étant pas de tout repos).
Notons aussi, que lorsqu'on a appris à construire un triangle d'or à partir de O et A donnés, il sera facile de construire le triangle d'or correspondant à O' et A' donnés. (voir le paragraphe suivant pour la mise en oeuvre).
Cela signifie donc que CABRI détermine seul la similitude transformant O et A en O' et A', ce qui me parait être très important pour montrer l'intérêt de CABRI en Terminale S : implicitement CABRI fait opérer une similitude dès qu'on déplace un point de base (libre), par exemple ici le point A, la figure en dépendant se déformant au cours du déplacement.

CONSTRUCTION DE TRIANGLES D'OR SEMBLABLES

Utilisation de la macro AIGORD

Nettoyer l'écran. Créer deux points A et C
Sélectionner dans le menu CONSTRUCTION la macro AIGORD .
Cliquer sur A puis C : vous obtenez un triangle d'or aigu.

Nommez éventuellement B le troisième sommet.
Sélectionnez à nouveau AIGORD . Cliquer sur C puis B : vous devez obtenir la figure ci-contre
Recommencez pour obtenir la figure suivante où les divers triangles sont les images itérées de ABC par la similitude qui transforme ABC en CDB . On localise, me semble t-il, le centre de cette similitude nécessairement intérieur aux divers triangles construits.

Recommencez pour obtenir la figure suivante où les divers triangles sont les images itérées de ABC par la similitude qui transforme ABC en CDB . On localise, me semble t-il, le centre de cette similitude nécessairement intérieur aux divers triangles construits.

Il ne reste plus, en Terminale S , qu'à s'attaquer à la détermination précise de ce centre à l'aide d'arcs capables. Exercice classique mais un peu plus délicat que pour les rectangles d'or. On peut là encore utiliser CABRI en parallèle à la construction papier-crayon .

L'angle (-3pi/5) et le rapport (1/phi) se déterminent sans difficulté.

SUITE ....