
|
Nombres de triangles ; Aires des triangles |
Nombre de triangles à chaque étape :

Voir un des modules qui décompte les triangles au cours des diverses étapes .
Aires des triangles d’or du pavage :
Quand on découpe le triangle d'or initial , on obtient deux triangles d'or : l'un aigu l'autre obtus. Quelles sont leurs aires ?
Un calcul élémentaire ou l'utilisation de la similitude évoquée plus haut montre que si l'on appelle Ta0 le triangle initial , Ta1 le triangle aigu et To1 le triangle obtus du premier découpage , on a :
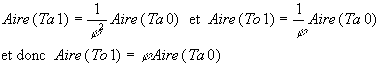
A l'étape suivante on aura en découpant le triangle obtus To1 :
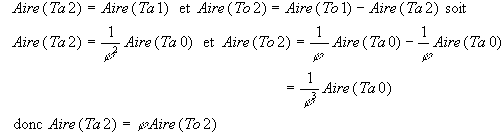
A chaque étape , ce sont alternativement les triangles aigus ou obtus qui ont la plus grande aire et l'on a :
et comme Aire(Tmin) était égale à Aire(Tmax) de l'étape précédente , les aires des deux types de triangles d'un pavage pour un degré donné sont deux termes consécutifs d'une suite géométrique de raison 1/j et de premier terme Aire(Ta0).
OU DE MANIERE PLUS ELEMENTAIRE :
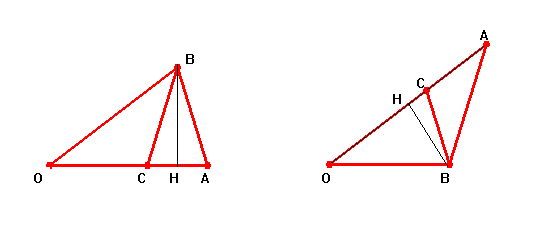
Les trois triangles OAB (=Ta0) , BAC (=Ta1) et OBC (=To1) ont même hauteur BH .
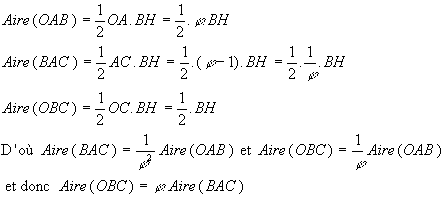
La démonstration est identique dans les deux cas puisque OA,OC,AC sont dans les mêmes rapports
( proportionnels à j ,1,,j-1=1/j ).Remarquons que les trois nombres Aire(OAB),Aire(OBC),Aire(ABC) sont trois termes consécutifs d'une suite géométriques de raison 1/j , et que , lors d'une étape du pavage de Penrose , le découpage d'un triangle d'un certain type ( d'aire maximum ) se fait donc dans un rapport égal au nombre d'or j ( aire du triangle de même type proportionnelle à 1, aire du triangle de l'autre type proportionnelle à j ).
C'est-à-dire :
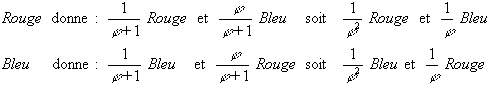
Si l'on s'intéresse uniquement à l'aire maximale
à une étape donnée : cette aire est une suite géométrique de raison 1/j et
.
Or la somme des aires est constante est vaut
et

Rapport des aires de tous les triangles aigus d'une part , obtus d'autre part :
Considérons plutôt le rapport aires minimales / aires maximales .

Cela montre que la poursuite du pavage n'a pas pour objectif de faire en sorte que les petits triangles compensent leur petite aire par un plus grand nombre , ni que, en terme de couleurs, on aille vers une couleur moyenne entre le rouge et le bleu , en effet le rapport ROUGE/BLEU est alternativement
et il n'admet pas de limite lorsque n tend vers l'infini .
Par contre ,si n est pair ,
Cette différence de comportement suivant la parité de n est bien visible sur les images montrant l'évolution du pavage dans les pages qui précèdent : les triangles de gauche obtenus pour n pair ont une dominante rouge alors que les triangles de droite obtenus pour n impair ont une dominante bleue ( visible même pour n=15 ou n=16 malgré le fait que ce sont les frontières en gris qui prennent de l'importance et estompent les couleurs des triangles ).
Remarquons encore que , pour n pair et assez grand,
