![]()
Les angles des losanges étant respectivement pi/5 , 2pi/5 ,3pi/5 ,4pi/5 , tout assemblage de ces losanges donne des cotés dont les angles avec une direction initiale est un multiple de pi/5 .
On peut donc rechercher quels sont les losanges dont un coté est parallèle à une direction donnée ( déterminée par l'angle polaire 0 , pi/5 , 2pi/5 ,3pi/5 ,4pi/5 ou 0 , pi/5, 2pi/5, -pi/5 , -2pi/5 ).
On obtient des "rubans" de losanges qui "zigzaguent" autour d'une droite dont la direction est perpendiculaire à la direction des cotés parallèles. Ces rubans sont sans éléments communs et "parallèles", les droites "axes moyens" des rubans étant parallèles et relativement équidistantes, du moins au vu des images obtenues. De plus il y a cinq directions de rubans .
Un module du programme permet d'obtenir ces rubans dans un triangle, un décagone, un plan. Dans le cas d'un décagone, il serait intéressant d'imprimer l'image sur transparent de façon à pouvoir superposer plusieurs d'entre elles et constater que les rubans de 4 directions recouvrent tout le décagone. En effet si l'on considère les rubans de quatre directions de cotés, tout losange du pavage , ayant deux cotés, appartient à au moins un ruban d'une des quatre directions données .
Par contre la superposition des rubans de trois directions ne recouvre pas tout le décagone et laisse des losanges isolés dont la répartition est assez régulière tout en n'étant pas périodique. Voir un diaporama sous PowerPoint
Le fait qu'il existe un axe moyen pour chaque ruban ne semble pas exceptionnel :
En effet, si l'on accolait au hasard des losanges d'or dont un coté a une direction fixée et
que l'on s'intéresse à l'écart des milieux du deuxième coté de direction donnée par rapport à la médiatrice du premier coté du premier triangle, on montre que cet écart a une espérance nulle quelque soit le nombre de losanges accolés.
Dans le plan, il est possible d'obtenir des rubans aussi longs que l'on veut (n'oubliez pas la similitude qui permet d'atteindre par un triangle d'or tout point du plan ). Si l'on prouve que ces rubans ne sont pas bornés, cela signifie qu'il existe une translation qui transforme une frontière du ruban dans l'autre. Dans ces conditions on peut enlever ce ruban et obtenir cependant un pavage du plan (voir un diaporama sous PowerPoint à ce sujet). De même il est possible d'accoler à un ruban un deuxième ruban identique ou même plusieurs . Ces opérations ne peuvent rendre le pavage périodique et ainsi on peut obtenir des pavages non périodiques du plan à priori différents de ceux obtenus par l'algorithme décrit plus haut.
La présence de ces rubans montre qu'il est possible de réaliser un escalier dont les marches auraient la forme des zones inter-rubans (escalier peu commode à descendre sans doute! )
Une autre question à laquelle je n'ai pas de réponse : Le long d'un ruban se succèdent des losanges étroits et larges ( qu'on pourrait coder 0 et 1 ou plutôt 1 , 2 , -1 , -2 pour tenir compte des orientations ) : ces losanges sont-ils répartis suivant une loi bien précise ou ... au hasard ( non sûrement pas )? Retrouve-t-on la même séquence dans deux rubans parallèles ? Oui, mais quelle est la longueur de la plus grande séquence présente dans deux rubans parallèles ? C'est sans doute une question à laquelle Penrose et ceux qui se sont intéressés à ces pavages apériodiques ont déjà répondu, mais je n'ai pas eu le temps de consulter les documents .
![]()
RUBANS DE LOSANGES D'OR ACCOLES AU HASARD
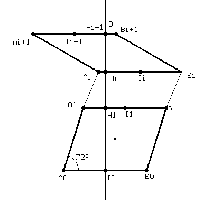
On se propose de fabriquer un ruban de losanges d'or (larges ou étroits) accolés par leurs cotés parallèles, le choix de chaque losange étant fait au hasard parmi les deux types, la position (gauche ou droite) étant elle aussi choisie au hasard, ces choix étant
indépendants des choix précédents . Nous étudierons l'écart des losanges par rapport au coté initial ou plutôt par rapport à la médiatrice du coté initial .
Considérons le premier losange construit sur le segment [A0 B0] :
si teta est égal à l'un des nombres pi/5 , 2pi/5 , 3pi/5 , 4pi/5 alors d1 = H1I1 =c cos teta où c=A0 B0.
Si D1 est la variable aléatoire correspondante, D1 prend les valeurs c cos(pi/5), c cos(2pi/5), c cos(3pi/5)=- c cos(2pi/5), c cos(4pi/5)= - c cos(pi/5) avec les probabilités 1/4. Donc D1 est centrée et son espérance est E(D1 ) = 0 .
Si l'on répète cette épreuve n fois en accolant n losanges :
Soit Di l'écart entre Ii et Ii+1. Di suit la même loi que D1 et E(Di ) = 0 .
L'écart En entre I0 et In est la somme des Di : En = D1 + D2 +...+ Dn .
On a donc E(En ) = E(D1 )+...+E( Dn ) = n x 0 = 0 .
Ce qui signifie que, quelque soit le nombre n de losanges d'or accolés , en
moyenne, le dernier milieu se trouve sur la médiatrice du coté initial , et donc que, en
moyenne, cette droite est axe moyen du ruban .
Ceci ne dépend pas du fait qu'il s'agisse de losanges d'or et est vrai pour les rubans
constitués de deux types de losanges (les côtés des deux types de losanges étant
isométriques ).
Les pavages de Penrose respectent donc cette propriété qui n'est peut-être pas aussi remarquable que ce que nous l'avons dit. Disons cependant que dans un ruban de Penrose, le ruban ne s'écarte jamais trop de cet axe médian (succession de 2 losanges au maximum à gauche ou à droite), alors que ce pourrait être le cas dans un ruban fabriqué de manière aléatoire.