A la recherche des symétries, des périodicités d'un pavage de Penrose .

Recherche du domaine stable par symétrie par rapport à un axe autre que celui du cerf-volant, puis par rotation d'angle 2pi/5, et enfin par toutes les isométries qui laissent un pentagone invariant .

APPROCHE de l'existence d'éléments de SYMETRIE

Point de départ : Dans le pavage d'ordre 1 du triangle initial , la présence du cerf-volant qui admet un axe de symétrie . Lorsque le degré augmente apparaît un deuxième "axe" ( qui n'est pas axe de symétrie ) mais qui tend à le devenir de plus en plus . Autrement dit il existe un sous-ensemble du cerf-volant globalement invariant dans cette deuxième réflexion. Cela est assez net à partir de l'ordre 8, comme nous l'avions noté dans l'étude de l'évolution du pavage.

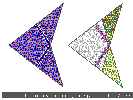Nous présentons des images obtenues par le programme CERFVOL qui affiche dans un premier temps le triangle d'or et son pavage, puis le triangle symétrique par rapport au "pseudo-axe", et enfin superpose les deux pavages dans deux modes: le mode "andput" où sont affichées les zones ayant même couleur dans leur couleur et le mode "Xorput" où les zones ayant même couleur sont affichées en blanc . La présence des deux images cote à cote permet de mieux distinguer le domaine invariant du domaine où les deux pavages ne coïncident pas . On constate que le domaine invariant est croissant avec le degré et que les zones de non-coïncidence semblent avoir pour axe moyen deux segments dont la position par rapport au triangle initial n'est pas quelconque .

Il n'y a ensuite qu'un pas à franchir pour déterminer le domaine invariant par rotation d'angle 4pi/5 (les deux axes formant un angle de 2pi/5) ou plutôt de 2pi/5 , puisque la présence de deux axes de symétrie entraine l'existence d'un troisième , puis d'un quatrième et d'un cinquième ....

On est donc amené à considérer toutes les isométries qui laissent invariant un pentagone , pentagone que l'on découvre comme ayant pour cotés les "axes moyens" des zones de non-coïncidences dont on parlait précédemment .

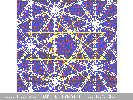
images disponibles dans le répertoire IMAGCH9 :

La plupart des images concernent les pavages de Penrose (algorithme n° 1), mais d'autres algorithmes sont présentés pour mettre en évidence les différences .

Dans le cas des pavages de Penrose présentés ici , on voit bien l'ensemble des " zones apériodiques " en blanc (ou en noir pour la dernière image, deux réseaux correspondants à deux degrés de profondeur consécutifs) : ces réseaux ont une structure pentagonale . En effet cet ensemble est globalement invariant par les isométries du pentagone, s'il en était autrement cela signifierait qu'une zone de non-coïncidence est transformée par une des isométries en une zone invariante, ce qui est exclu.